# The Measurement Problem The "Problem of Measurement" in quantum mechanics has been defined in various ways, originally by physicists, and more recently by philosophers of physics who question the "foundations of quantum mechanics." Many physicists define the "problem" of measurement simply as the _logical_ contradiction between _two "laws"_ that appear to contradict one another when describing the motion or "evolution" in space and time of a quantum system. The first motion "law" is the [irreversible](https://www.informationphilosopher.com/problems/reversibility/), non-unitary, discrete, discontinuous, and [indeterministic](https://www.informationphilosopher.com/freedom/indeterminism.html) or "random" [collapse](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) of the wave function. [P.A.M.Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/) called it his [Projection Postulate](https://www.informationphilosopher.com/solutions/scientists/dirac/#postulate). A few years later [John von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/) called this [Process 1](https://www.informationphilosopher.com/solutions/scientists/neumann/#process1%22) At the moment of this "collapse" new information appears in the universe. It is this information that is the "outcome" of a measurement. [Werner Heisenberg](https://www.informationphilosopher.com/problems/measurement/solutions/scientists/hesenberg) saw this law as "acausal" and "statistical." The second motion "law" is the [time reversible](https://www.informationphilosopher.com/problems/reversibility/), unitary, continuous, and [deterministic](https://www.informationphilosopher.com/freedom/determinism.html) evolution of the Schrödinger equation (von Neumann's Process 2). Nothing observable happens during this motion. No new information appears that might be observed. [John von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/) was perhaps first to see a _logical_ problem with these two distinct (indeed, opposing) processes. Later physicists saw no mechanism that can _explain_ the transition from a continuous evolution to the discontinuous state change. The standard formalism of quantum mechanics says that the _deterministic_ continuous evolution "law" describes only the [probability](https://www.informationphilosopher.com/freedom/probability.html) of the _indeterministic_ "collapse" of the second "law." [Max Born](https://www.informationphilosopher.com/solutions/scientists/born/) summarized this conflict as a paradox: "The motion of the particle follows the laws of probability, but the probability itself propagates in accord with causal laws." The mathematical formalism of quantum mechanics simply provides no way to _predict_ when the wave function stops evolving in a predictable _deterministic_ fashion and _indeterministically_collapses randomly and unpredictably. Starting with Von Neumann, physicists have claimed that the collapse must occur when a microscopic quantum system interacts with a macroscopic (approximately classical) measuring apparatus. The apparatus "measures" the quantum system, producing the [irreversible](https://www.informationphilosopher.com/problems/reversibility/) information that can be seen by an observer. But we must note that this classical measurement apparatus has been only an _ad hoc_ assumption that has never produced a _model_ of its inner workings. Some theorists have added extra non-linear terms to the [Schrödinger equation](https://www.informationphilosopher.com/quantum/equation/) to force the collapse. But these _ad hoc_ extra terms still do not predict the time of the collapse exactly, nor do they describe what is happening during the collapse process. So ultimately, the collapse happens at a random time and at that time macroscopically observable _new information_ appears [irreversibly](https://www.informationphilosopher.com/problems/reversibility/), as first claimed by von Neumann. To describe the problem of measurement more fully we need diverse concepts in quantum physics such as: - "Wave functions" (a/k/a _eigenfunctions_ which are _probability amplitudes_) evolving unitarily and [deterministically](https://www.informationphilosopher.com/freedom/determinism.html) (preserving constant information) according to the linear [Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/) equation, ([John von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/) called this his **[Process 2](https://www.informationphilosopher.com/solutions/scientists/neumann/#process2)**), - "[Superpositions](https://www.informationphilosopher.com/quantum/superposition/)" of quantum states (a/k/a _eigenstates_). These are linear combinations of wave functions with complex coefficients that carry coherent _phase_ information and produce _interference_ effects ([P.A.M. Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/) called this his [_principle of superposition_), ](https://www.informationphilosopher.com/quantum/principles/#superposition) [](https://www.informationphilosopher.com/quantum/principles/#superposition)- ["Quantum jumps" between states accompanied by the](https://www.informationphilosopher.com/quantum/principles/#superposition) ["collapse" of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) into a particular state that can create or destroy information (Dirac called this his _[projection postulate](https://www.informationphilosopher.com/quantum/principles/#postulate)_, [von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/) called it **[Process 1](https://www.informationphilosopher.com/solutions/scientists/neumann/#process1)**), - "[Probabilities](https://www.informationphilosopher.com/freedom/probability.html) "of collapses and quantum jumps are given by the square of the absolute value of the wave function (the _probability amplitudes_) for a given state, - Values for the possible measurement "outcomes" given by the _eigenvalues_ associated with the _eigenstates_ of the combined measuring apparatus and measured system (Dirac called it his [_axiom of measurement_](https://www.informationphilosopher.com/quantum/principles/#axiom). Others call it the _eigenstate-eigenvalue_ link), - The [Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/) [indeterminacy](https://www.informationphilosopher.com/freedom/indeterminacy.html) principle. The original problem, said to be a consequence of [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/)'s "[Copenhagen interpretation](https://www.informationphilosopher.com/introduction/physics/copenhagen_interpretation.html)" of quantum mechanics, was to explain how our measuring instruments, which are usually _macroscopic_ objects and treatable with classical physics, can give us [information](https://www.informationphilosopher.com/introduction/information/) about the _microscopic_ world of atoms and subatomic particles like electrons and photons. Bohr's idea of ["complementarity"](https://www.informationphilosopher.com/introduction/physics/complementarity.html) insisted that a specific experiment could reveal only partial information - for example, either a particle's position or the wavelength of the particle's "dual" complementary wave nature. . "Exhaustive" information requires complementary experiments, for example to determine a particle's position and also its momentum (within the limits of [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/)'s indeterminacy principle). In general, a quantum system with internal structure consists of a number of internal quantum states that can be arranged in a "ground state" with a minimal energy and a number of "excited" states, with increasing "energy levels." As [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) showed in 1916, the "population" of each energy level (the probable number of systems in that state) decreases with the energy _E_ of the level according to the "Boltzmann factor," _e-E/kT_. [P.A.M. Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/)'s _transformation theory_ of quantum mechanics describes quantum states as vectors in an abstract space called a "Hilbert space." Others define the measurement problem as the failure to observe _macroscopic superpositions_. For example, the paradoxical idea of [Schrödinger's cat](https://www.informationphilosopher.com/solutions/experiments/schrodingerscat/) being in a superposition of "dead" and "alive" states. [Decoherence](https://www.informationphilosopher.com/knowledge/decoherence.html) theorists. e.g., [H. Dieter Zeh](https://www.informationphilosopher.com/solutions/scientists/zeh/) and [Wojciech Zurek](https://www.informationphilosopher.com/solutions/scientists/zurek/), use various non-standard interpretations of quantum mechanics that deny the projection postulate, quantum jumps, and even the existence of particles. They define the measurement problem as the failure to observe macroscopic superpositions. The [deterministic](https://www.informationphilosopher.com/freedom/determinism.html), _linear_, and _unitary_ time evolution of the wave function according to the Schrödinger wave equation should produce such macroscopic superpositions, they claim. [Information physics](https://www.informationphilosopher.com/introduction/physics/) treats a measuring apparatus quantum mechanically by describing parts of it as in a _metastable_ state like the excited states of an atom, the critically poised electrical potential energy in the discharge tube of a [Geiger counter](https://www.informationphilosopher.com/solutions/experiments/geiger_counter/), or the supersaturated water and alcohol molecules of a Wilson [cloud chamber](https://www.informationphilosopher.com/solutions/experiments/cloud_chamber/). (The pi-bond orbital rotation from cis- to trans- in the light-sensitive retinal molecule is an example of a critically poised apparatus). Excited (metastable) states are poised to collapse when an electron (or photon) collides with the sensitive detector elements in the apparatus. This collapse is macroscopic and _irreversible_, generally a cascade of quantum events that release large amounts of energy, increasing the (Boltzmann) entropy. But in a "measurement" there is also a local decrease in the entropy (negative entropy or information). The global entropy increase is normally orders of magnitude more than the small local decrease in entropy (an increase in stable information or Shannon entropy) that constitutes the "measured" experimental data available to human observers. The creation of new information in a measurement thus follows the same two core processes of [all information creation](https://www.informationphilosopher.com/introduction/creation/) - quantum cooperative phenomena and thermodynamics. These two are involved in the formation of microscopic objects like atoms and molecules, as well as macroscopic objects like galaxies, stars, and planets. According to the _correspondence principle_, all the laws of quantum physics asymptotically approach the laws of classical physics in the limit of large quantum numbers and large numbers of particles. Quantum mechanics can be used to describe large macroscopic systems. Does this mean that the positions and momenta of macroscopic objects are uncertain? Yes, it does, although the uncertainty becomes vanishingly small for large objects, it is not zero. [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/) used the uncertainty of macroscopic objects to defeat [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/)'s several objections to quantum mechanics at the 1927 Solvay conference. But Bohr and Heisenberg also insisted that a measuring apparatus must be a regarded as a purely classical system. They can't have it both ways. Can the macroscopic apparatus also be treated by quantum physics or not? Can it be described by the Schrödinger equation? Can it be regarded as in a superposition of states? The most famous examples of macroscopic superposition are perhaps [Schrödinger's Cat](https://www.informationphilosopher.com/solutions/experiments/schrodingerscat/), which is claimed to be in a superposition of live and dead cats, and the [Einstein-Podolsky-Rosen experiment](https://www.informationphilosopher.com/solutions/experiments/EPR/), in which entangled electrons or photons are in a superposition of two-particle states that collapse over macroscopic distances to exhibit properties "[nonlocally](https://www.informationphilosopher.com/problems/nonlocality/)" suggesting "actions-at-a-distance" at speeds faster than the speed of light. These treatments of macroscopic systems with quantum mechanics were intended to expose inconsistencies and incompleteness in quantum theory. Some of the critics hoped to restore [determinism](https://www.informationphilosopher.com/freedom/determinism.html) and "local reality" to physics. They resulted in some strange and extremely popular "[mysteries](https://www.informationphilosopher.com/freedom/mysteries.html)" about "quantum reality," such as the "many-worlds" interpretation, "hidden variables," and signaling faster than the speed of light. We develop a quantum-mechanical treatment of macroscopic systems, especially a measuring apparatus, to show how it can create new information. If the apparatus were describable only by classical deterministic laws, no new information could come into existence. In a deterministic universe, information is a constant at all times, like the total of matter and energy. The apparatus need only be [adequately determined](https://www.informationphilosopher.com/freedom/adequate_determinism.html), that is to say, "classical" _to a sufficient degree of accuracy_. How Classical Is a Macroscopic Measuring Apparatus? As Landau and Lifshitz described it in their 1958 textbook _Quantum Mechanics_" > The possibility of a quantitative description of the motion of an electron requires the presence also of physical objects which obey classical mechanics to a sufficient degree of accuracy. If an electron interacts with such a "classical object", the state of the latter is, generally speaking, altered. The nature and magnitude of this change depend on the state of the electron, and therefore may serve to characterise it quantitatively... > > We have defined "apparatus" as a physical object which is governed, with sufficient accuracy, by classical mechanics. Such, for instance, is a body of large enough mass. However, it must not be supposed that apparatus is necessarily macroscopic. Under certain conditions, the part of apparatus may also be taken by an object which is microscopic, since the idea of "with sufficient accuracy" depends on the actual problem proposed. > > Thus quantum mechanics occupies a very unusual place among physical theories: it contains classical mechanics as a limiting case [correspondence principle], yet at the same time it requires this limiting case for its own formulation. > > (_Quantum Mechanics_, Lev Landau and Evgeny Lifshitz, pp.2-3 The measurement problem was analyzed mathematically in 1932 by [John von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/). Following the work of [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/) and [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/bohr/), von Neumann divided the world into a microscopic (atomic-level) quantum system and a macroscopic (classical) measuring apparatus. Von Neumann explained that _two fundamentally different processes are going on_ in quantum mechanics. 1. A _non-causal **process 1**_, in which the measured electron winds up _randomly_ in one of the possible physical states (eigenstates) of the measuring apparatus plus electron. This process came to be called the [_collapse of the wave function_](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) or the _reduction_ of the wave packet. The probability for finding the electron in a specific eigenstate is given by the square of the coefficients **c_n_** of the expansion of the original system state (wave function **ψ**) in an infinite set of wave functions **φ** that represent the eigenfunctions of the measuring apparatus plus electron. This is as close as we get to a description of the motion of the particle aspect of a quantum system. According to von Neumann, the particle simply shows up somewhere as a result of a measurement. _[Information physics](https://www.informationphilosopher.com/introduction/physics/)_ says that the particle "shows up" only when a new stable information structure is created, information that subsequently _can be observed_. **Process 1b**. The information created in Von Neumann's Process 1 will only be stable if an amount of positive entropy greater than the negative entropy in the new information structure is transported away, in order to satisfy the second law of thermodynamics. 2. A _causal **process 2**_, in which the electron wave function **ψ** evolves _deterministically_ according to Schrödinger's equation of motion for the wavelike aspect. (ih/2π) ∂**ψ**/∂t = **Hψ**. This evolution describes the motion of the probability amplitude wave **ψ** between measurements. The wave function exhibits interference effects. But interference is destroyed if the particle has a definite position or momentum. The particle path _can not be observed_. Von Neumann claimed there is another major difference between these two processes. Process **1** is thermodynamically _irreversible_. Process **2** is _reversible_. This confirms the fundamental connection between quantum mechanics and thermodynamics that _information physics_ finds at the heart of all information creation. _Information physics_ can show quantum mechanically how **process 1** creates information. Indeed, something like **process 1** is always involved when any information is created, whether or not the new information is ever "observed" by a human being. Process **2** is [deterministic](https://www.informationphilosopher.com/freedom/determinism.html) and _information preserving_. Just as the _new information recorded in the measurement apparatus cannot subsist_ unless a compensating amount of _entropy is transferred away_ from the new information, something similar to Process 1b must happen in the mind of an observer if the new information is to constitute an "observation." It is only in cases where information persists long enough for a human being to observe it that we can properly describe the observation as a "[measurement](https://www.informationphilosopher.com/problems/measurement/)" and the human being as an "observer." So, following von Neumann's "process" terminology, we can complete his theory of the measuring process by adding an anthropomorphic > **Process 3** - a conscious observer _recording_ new _information_ in a mind. This is only possible if there are two local reductions in the entropy (the first in the measurement apparatus, the second in the mind), both balanced by even greater increases in positive entropy that must be transported away from the apparatus and the mind, so the overall increase in entropy can satisfy the second law of thermodynamics. For some physicists, it is the [wave-function collapse](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) that gives rise to the _problem of measurement_ because its randomness prevents us from including it in the mathematical formalism of the deterministic Schrödinger equation in **process 2**. The randomness that is irreducibly involved in all information creation lies at the heart of [human freedom](https://www.informationphilosopher.com/freedom/). It is the "free" in "[free will](https://www.informationphilosopher.com/freedom/free_will.html)." The "will" part is as [adequately and statistically determined](https://www.informationphilosopher.com/freedom/adequate_determinism.html) as any macroscopic object. Designing a Quantum Measurement Apparatus The first step is to build an apparatus that allows different components of the wave function to evolve along distinguishable paths into different regions of space, where the different regions correspond to (are correlated with) the physical properties we want to measure. We then can locate a detector in these different regions of space to catch particles travelling a particular path. We do not say that the system is on a particular path in this first step. That would cause the probability amplitude wave function to collapse. This first step is _reversible_, at least in principle. It is deterministic and an example of von Neumann process 2. Let's consider the separation of a beam of photons into horizontally and vertically polarized photons by a birefringent crystal. We need a beam of photons (and the ability to reduce the intensity to a single photon at a time). Vertically polarized photons pass straight through the crystal. They are called the ordinary ray, shown in red. Horizontally polarized photons, however, are deflected at an angle up through the crystal, then exit the crystal back at the original angle. They are called the extraordinary ray, shown in blue.  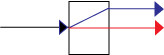Note that this first part of our apparatus accomplishes the separation of our two states into distinct physical regions. We have not actually measured yet, so a single photon passing through our measurement apparatus is described as in a linear combination (a superposition) of horizontal and vertical polarization states, > | _ψ_ > = ( 1/√2) | _h_ > + ( 1/√2) | _v_ >          (1) See the [Dirac Three Polarizers experiment](https://www.informationphilosopher.com/solutions/experiments/dirac_3-polarizers/) for more details on polarized photons. 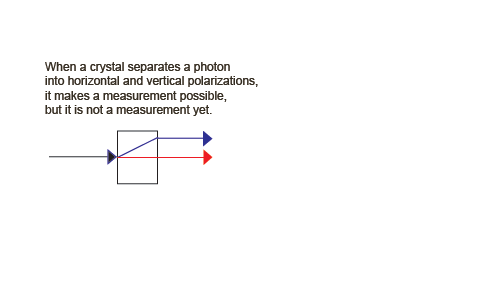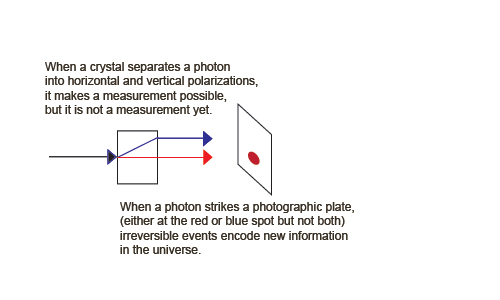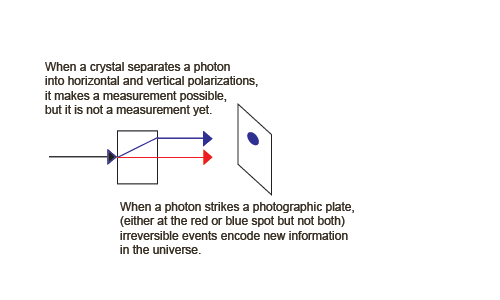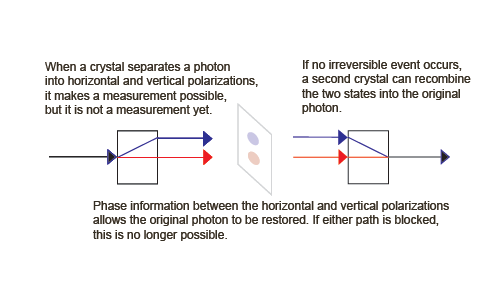An Information-Preserving, Reversible Example of Process 2 To show that process 2 is reversible, we can add a second birefringent crystal upside down from the first, but inline with the superposition of physically separated states,  Since we have not made a measurement and do not know the path of the photon, the phase information in the (generally complex) coefficients of equation (1) has been preserved, so when they combine in the second crystal, they emerge in a state identical to that before entering the first crystal (black arrow). Note that the two crystals can be treated classically, according to standard optics. An Information-Creating, Irreversible Example of Process 1 But now suppose we insert something between the two crystals that is capable of a measurement to produce observable information. We need a detector that locates the photon in one of the two rays. We can now create an information-creating, irreversible example of process 1. Suppose we insert something between the two crystals that is capable of a measurement to produce observable information. We need detectors, for example two charge-coupled devices that locate the photon in one of the two rays. We can write a quantum description of the CCDs, one measuring horizontal photons, | Ah > (shown as the blue spot), and the other measuring vertical photons, | Av > (shown as the red spot).  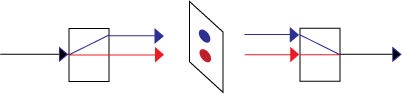We treat the detection systems quantum mechanically, and say that each detector has two eigenstates, e.g., | Ah0 >, corresponding to its initial state and correlated with no photons, and the final state | Ah1 >, in which it has detected a horizontal photon. When we actually detect the photon, say in a horizontal polarization state with statistical probability 1/2, two "collapses" or "jumps" occur. The first is the jump of the probability amplitude wave function | _ψ_ > of the photon in equation (1) into the horizontally polarized state | _h_ >. The second is the quantum jump of the horizontal detector from | Ah0 > to | Ah1 >. These two happen together, as the quantum states have become correlated with the states of the sensitive detectors in the classical apparatus. One can say that the photon has become entangled with the sensitive horizontal detector area, so that the wave function describing their interaction is a superposition of photon and apparatus states that cannot be observed independently. > | _ψ_ > + | Ah0 >      =>      | _ψ_, Ah0 >      =>      | _h_, Ah1 > These jumps destroy (unobservable) phase information, raise the (Boltzmann) entropy of the apparatus, and increase visible information (Shannon entropy) in the form of the visible spot. The entropy increase takes the form of a large chemical energy release when the photographic spot is developed (or a cascade of electrons in a CCD). Note that the birefringent crystal and the parts of the macroscopic apparatus other than the sensitive detectors are treated classically. We can animate these irreversible and reversible processes,  We see that our example agrees with Von Neumann. A measurement which finds the photon in a specific state _n_ is thermodynamically irreversible, whereas the deterministic evolution described by Schrödinger's equation is reversible as long as the photon is in a superposition of possible states. We thus establish a clear connection between a measurement, which increases the [information](https://www.informationphilosopher.com/introduction/information/) by some number of bits (Shannon entropy), and the necessary compensating increase in the (Boltzmann) entropy of the macroscopic apparatus, and the [cosmic creation process](https://www.informationphilosopher.com/introduction/creation/), where new particles form, reducing the entropy locally, and the energy of formation is radiated or conducted away as Boltzmann entropy. Note that the Boltzmann entropy can only be radiated away (ultimately into the night sky to the cosmic microwave background) because the expansion of the universe provides a sink for the entropy, as pointed out by [David Layzer](https://www.informationphilosopher.com/solutions/scientists/layzer/). Note also that this cosmic information-creating process requires no conscious observer. The universe is its own observer. The Boundary between the Classical and Quantum Worlds Some scientists ([John von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/) and [Eugene Wigner](https://www.informationphilosopher.com/solutions/scientists/wigner/), for example) have argued that in the absence of a conscious observer, or some "cut" between the microscopic and macroscopic world, the evolution of the quantum system and the macroscopic measuring apparatus would be described [deterministically](https://www.informationphilosopher.com/freedom/determinism.html) by Schrödinger's equation of motion for the wave function | _ψ_ + A > with the Hamiltonian **H** energy operator, > (ih/2π) ∂/∂t | _ψ_ + A > = **H** | _ψ_ + A >. Our quantum mechanical analysis of the measurement apparatus in the above case allows us to locate the "cut" or "Schnitt" between the microscopic and macroscopic world at those components of the "adequately classical and deterministic" apparatus that put the apparatus in an irreversible stable state providing new [information](https://www.informationphilosopher.com/introduction/information/) to the observer. [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) drew a diagram to show the various possible locations for what he called the "shifty split." [Information physics](https://www.informationphilosopher.com/introduction/physics/) shows us that the correct location for the boundary is the first of Bell's possibilities. 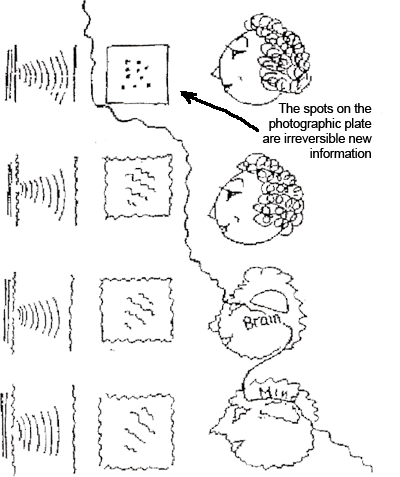>  The Role of a Conscious Observer In 1941, Carl von Weizsäcker described the measurement problem as an interaction between a Subject and an Object, a view shared by the philosopher of science [Ernst Cassirer](https://www.informationphilosopher.com/solutions/philosophers/cassirer/%22). Fritz London and Edmond Bauer made the strongest case for the critical role of a conscious observer in 1939: > So far we have only coupled one apparatus with one object. But a coupling, even with a measuring device, is not yet a measurement. A measurement is achieved only when the position of the pointer has been _observed_. It is precisely this increase of knowledge, acquired by observation, that gives the observer the right to choose among the different components of the mixture predicted by theory, to reject those which are not observed, and to attribute thenceforth to the object a new wave function, that of the pure case which he has found. > > We note the essential role played by the consciousness of the observer in this transition from the mixture to the pure case. Without his effective intervention, one would never obtain a new function. > > (_The Theory of Observation in Quantum Mechanics_, Fritz London and Edmond Bauer, in Wheeler and Zurek, p.251) In 1961, [Eugene Wigner](https://www.informationphilosopher.com/solutions/scientists/wigner/) made quantum physics even more subjective, claiming that a quantum measurement _requires_ a conscious observer, without which nothing ever happens in the universe. > When the province of physical theory was extended to encompass microscopic phenomena, through the creation of quantum mechanics, the concept of consciousness came to the fore again: it was not possible to formulate the laws of quantum mechanics in a fully consistent way without reference to the consciousness All that quantum mechanics purports to provide are probability connections between subsequent impressions (also called "apperceptions") of the consciousness, and even though the dividing line between the observer, whose consciousness is being affected, and the observed physical object can be shifted towards the one or the other to a considerable degree [cf., [von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/)] it cannot be eliminated. It may be premature to believe that the present philosophy of quantum mechanics will remain a permanent feature of future physical theories; it will remain remarkable, in whatever way our future concepts may develop, that the very study of the external world led to the conclusion that the content of the consciousness is an ultimate reality. > > (_Remarks on the Mind-Body Question_, Eugene Wigner, in Wheeler and Zurek, p.169) Other physicists were more circumspect. [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/) contrasted [Paul Dirac](https://www.informationphilosopher.com/problems/measurement/solutions/scientists/dirac/)'s view with that of Heisenberg: > These problems were instructively commented upon from different sides at the Solvay meeting, in the same session where Einstein raised his general objections. On that occasion an interesting discussion arose also about how to speak of the appearance of phenomena for which only predictions of statistical character can be made. The question was whether, as to the occurrence of individual effects, we should adopt a terminology proposed by Dirac, that we were concerned with a choice on the part of "nature," or, as suggested by Heisenberg, we should say that we have to do with a choice on the part of the "observer" constructing the measuring instruments and reading their recording. Any such terminology would, however, appear dubious since, on the one hand, it is hardly reasonable to endow nature with volition in the ordinary sense, while, on the other hand, it is certainly not possible for the observer to influence the events which may appear under the conditions he has arranged. To my mind, there is no other alternative than to admit that, in this field of experience, we are dealing with individual phenomena and that our possibilities of handling the measuring instruments allow us only to make a choice between the different complementary types of phenomena we want to study. > > (_Atomic Physics and Human Knowledge_, Niels Bohr, p.51) Landau and Lifshitz said clearly that quantum physics was independent of any observer: > In this connection the "classical object" is usually called apparatus, and its interaction with the electron is spoken of as measurement. However, it must be most decidedly emphasised that we are here not discussing a process of measurement in which the physicist-observer takes part. By measurement, in quantum mechanics, we understand any process of interaction between classical and quantum objects, occurring apart from and independently of any observer. > > (_Quantum Mechanics_, Lev Landau and Evgeny Lifshitz, p.2) [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/) agreed that what is observed is distinct from the observer: > If it were necessary to give all parts of the world a completely quantum-mechanical description, a person trying to apply quantum theory to the process of observation would be faced with an insoluble paradox. This would be so because he would then have to regard himself as something connected inseparably with the rest of the world. On the other hand,the very idea of making an observation implies that what is observed is totally distinct from the person observing it. > > (_Quantum Theory_, David Bohm, p.584) And [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) said: > It would seem that the [quantum] theory is exclusively concerned about 'results of measurement', and has nothing to say about anything else. What exactly qualifies some physical systems to play the role of 'measurer'? Was the wavefunction of the world waiting to jump for thousands of millions of years until a single-celled living creature appeared? Or did it have to wait a little longer, for some better qualified system...with a Ph.D.? If the theory is to apply to anything but highly idealised laboratory operations, are we not obliged to admit that more or less 'measurement-like' processes are going on more or less all the time, more or less everywhere? Do we not have jumping then all the time? > > (_Speakable and Unspeakable in Quantum Mechanics_, "Against Measurement," p. 216) Three Essential Steps in a "Measurement" and "Observation" We can distinguish three required elements in a measurement that can clarify the ongoing debate about the role of a conscious observer. 1. In standard quantum theory, the first required element is the [collapse of the wave-function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). This is the Dirac _projection postulate_ and von Neumann **Process 1**. However, the collapse might not leave a determinate record. If nothing in the environment is macroscopically affected so as to leave an indelible record of the collapse, we can say that no information about the collapse is created. The overwhelming fraction of collapses are of this kind. Moreover, information might actually be destroyed. For example, collisions between atoms or molecules in a gas that erase past information about their paths. 2. If the collapse occurs when the quantum system is entangled with a macroscopic measurement apparatus, a well-designed apparatus will also "collapse" into a correlated "pointer" state. As we showed above for photons, the detector in the upper half of a Stern-Gerlach apparatus will fire, indicating detection of an electron with spin up. As with photons, if the probability amplitude | ↑ > in the upper half does not collapse as the electron is detected, it can still be recombined with the probability amplitude | ↓ > in the lower half to reconstruct the unseparated beam. When the apparatus detects a particle, the second required element is that it produce a determinate record of the event. But this is impossible without an [irreversible](https://www.informationphilosopher.com/problems/reversibility/) thermodynamic process that involves: a) the creation of at least one bit of new information (negative entropy) and b) the transfer away from the measuring apparatus of an amount of positive entropy (generally much, much) greater than teh information created. Notice that no conscious observer need be involved. We can generalize this second step to an event in the physical world that was not designed as a measurement apparatus by a physical scientist, but nevertheless leaves an indelible record of the collapse of a quantum state. This might be a highly specific single event, or the macroscopic consequence of billions of atomic-molecular level of events. 3. Finally, the third required element is an indelible determinate record that can be looked at by an observer (presumably conscious, although the consciousness itself has nothing to do with the measurement). When we have all three of these essential elements, we have what we normally mean by a measurement and an observation, both involving a human being. When we have only the first two, we can say metaphorically that the "universe is measuring itself," creating an information record of quantum collapse events. For example, every hydrogen atom formed in the early recombination era is a record of the time period when macroscopic bodies could begin to form. A certain pattern of photons records the explosion of a supernova billions of light years away. When detected by the CCD in a telescope, it becomes a potential observation. Craters on the back side of the moon recorded collisions with solar system debris that could become observations only when the first NASA mission circled the moon.