# Entropy, Information, and Probability
For over sixty years, since I first read [Arthur Stanley Eddington](https://www.informationphilosopher.com/solutions/scientists/eddington/)'s _The Nature of the Physical World_, I have been struggling, as the "information philosopher," to _understand_ and to find simpler ways to _explain_ the concept of entropy.
Even more challenging has been to find the best way to teach the mathematical and philosophical connections between entropy and [information](https://www.informationphilosopher.com/introduction/information/). A great deal of the literature complains that these concepts are too difficult to understand and may have nothing to do with one another.
Finally, there is the important concept of _[probability](https://www.informationphilosopher.com/freedom/probability.html)_, with its implication of _[possibilities](https://www.informationphilosopher.com/freedom/alternative_possibilities.html)_, one or more of which may become an _actuality_.
[Determinist](https://www.informationphilosopher.com/freedom/determinism.html) philosophers (perhaps a majority) and scientists (a strong minority) say that we use probability and statistics only because our finite minds are incapable of understanding reality. Their idea of the universe is that it contains infinite information which only an infinite mind can comprehend. Our observable universe contains a very large but finite amount of information. Entropy is a measure of that lost energy.
A very strong connection between entropy and probability is obvious because [Ludwig Boltzmann](https://www.informationphilosopher.com/solutions/scientists/boltzmann/)'s formula for entropy _S_ = log_W_, where W stands for _Wahrscheinlichkeit_, the German for probability. We believe that [Rudolf Clausius](https://www.informationphilosopher.com/solutions/scientists/clausius/), who first defined and named entropy, gave it the symbol _S_ in honor of [Sadi Carnot](https://www.informationphilosopher.com/solutions/scientists/carnot/), whose study of heat engine efficiency showed that some fraction of available energy is always wasted or dissipated, only a part can be converted to mechanical work.
is mathematically identical to [Claude Shannon](https://www.informationphilosopher.com/solutions/scientists/shannon/)'s expression for information _I_, but with a minus sign and different dimensions.
Boltzmann entropy: _S = _k_ ∑ pi ln pi_. Shannon information: _I = - ∑ pi ln pi_.
_Boltzmann entropy_ and _Shannon entropy_ have different dimensions (_S_ = joules/°K,
_I_ = dimensionless "bits"), but they share the "mathematical isomorphism" of a logarithm of probabilities, which is the basis of both Boltzmann's and [Gibbs](https://www.informationphilosopher.com/solutions/scientists/gibbs/)' statistical mechanics..
The first entropy is material, the latter mathematical - indeed purely _immaterial_ information.
But they have deeply important connections which information philosophy must sort out and explain.
First, both Boltzmann and Shannon expressions contain _probabilities_ and _statistics_. Many philosophers and scientists deny any _ontological_ [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html), such as the [chance](https://www.informationphilosopher.com/chance/) in quantum mechanics discovered by [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/index.html#chance) in 1916. They may accept an _epistemological_ [uncertainty](https://www.informationphilosopher.com/freedom/uncertainty.html), as proposed by [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/) in 1927.
Today many thinkers propose [chaos](https://www.informationphilosopher.com/freedom/chaos.html) and [complexity](https://www.informationphilosopher.com/freedom/chaos.html) theories (both theories are completely _deterministic_) as adequate explanations, while they deny ontological [chance](https://www.informationphilosopher.com/chance/). Ontological chance is the basis for creating any information structure. It explains the variation in species needed for Darwinian evolution. It underlies human [freedom](https://www.informationphilosopher.com/freedom/) and the [creation](https://www.informationphilosopher.com/introduction/creation/) of new ideas.
In statistical mechanics, the summation ∑ is over all the possible distributions of gas particles in a container. If the number of distributions is _W_ , and the probability of all distributions is the same, the pi are all equal to 1/_W_ and entropy is maximal: _S = k_ ∑ 1/_W_ ln 1/_W_, so _S = k_ ln _W_.
In the communication of information, _W_ is the number of possible messages. If the probability of all messages is the same, pi are identical, _I_ = - ln_W_. If there are _N_ possible messages, then _N_ bits of information are communicated by receiving one of them.
On the other hand, if there is only one possible message, its probability is unity, and the information content is _1_ ln _0_ = zero.
If there is only one possible message, no new information is communicated. This is the case in a [deterministic](https://www.informationphilosopher.com/freedom/determinism.html) universe, where past events completely [cause](https://www.informationphilosopher.com/freedom/causality.html) present events. The information in a deterministic universe is a constant of nature. Religions that include an omniscient god often believe all that information is in God's mind.
Note that if there are no [alternative possibilities](https://www.informationphilosopher.com/freedom/alternative_possibilities.html) in messages, Shannon (following his Bell Labs colleague [Ralph Hartley](https://www.informationphilosopher.com/solutions/scientists/hartley/)) says there can be no new information. We conclude that the creation of new information structures in the universe is only possible because the universe is in fact [indeterministic](https://www.informationphilosopher.com/freedom/indeterminism.html) and our futures are _open_ and [free](https://www.informationphilosopher.com/freedom/).
Thermodynamic entropy involves matter and energy, Shannon entropy is entirely mathematical, on one level purely _immaterial_ information, though it cannot exist without "negative" thermodynamic entropy.
It is true that information is neither matter nor energy, which are conserved constants of nature (the first law of thermodynamics). But information needs matter to be embodied in an "information structure." And it needs ("free") energy to be communicated over Shannon's information channels.
Boltzmann entropy is intrinsically related to "negative entropy." Without pockets of negative entropy in the universe (and out-of-equilibrium free-energy flows), there would no "information structures" anywhere.
Pockets of negative entropy are involved in the _creation_ of everything interesting in the universe. It is a [cosmic creation process](https://www.informationphilosopher.com/introduction/creation/) _without a creator_.
## Visualizing Information
There is a mistaken idea in statistical physics that any particular distribution or arrangement of material particles has exactly the same information content as any other distribution. This is an anachronism from nineteenth-century [deterministic](https://www.informationphilosopher.com/freedom/determinism.html) statistical physics.
| | | |
|---|---|---|
|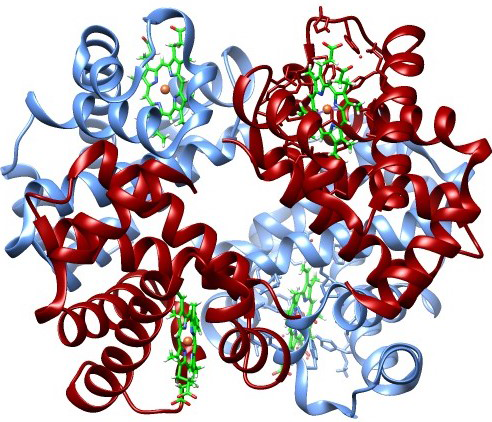|||
|Hemoglobin|Diffusing|Completely Mixed Gas|
If we measure the positions in _phase space_ of all the atoms in a hemoglobin protein, we get a certain number of bits of data (the x, y, z, vx, vy, vz values). If the chemical bonds are all broken allowing atoms to diffuse, or the atoms are completely randomized into an equilibrium gas with maximum entropy, we get different values, but the same amount of data. Does this mean that any particular distribution has exactly the same information?
This led many statistical physicists to claim that information in a gas is the same wherever the particles are, _Macroscopic_ information is not lost, it just becomes _microscopic_ information that can be completely recovered if the motions of every particle could be reversed. [Reversibility](https://www.informationphilosopher.com/problems/reversibility/) allows all the gas particles to go back inside the bottle.
But the [information](https://www.informationphilosopher.com/introduction/information/) in the hemoglobin is much higher and the disorder (entropy) near zero. A human being is not just a "bag of chemicals," despite plant biologist [Anthony Cashmore](https://www.informationphilosopher.com/solutions/scientists/cashmore/). Each atom in hemoglobin is not merely in some volume limited by the uncertainty principle ℏ3, it is in a specific quantum cooperative relationship with its neighbors that support its biological function. These precise positional relationships make a passive linear protein into a properly folded active enzyme. Breaking all these quantum chemical bonds destroys [life](https://www.informationphilosopher.com/problems/life/).
Where an information structure is present, the entropy is low and Gibbs free energy is high.
When gas particles can go anywhere in a container, the number of possible distributions is enormous and entropy is maximal. When atoms are bound to others in the hemoglobin structure, the number of possible distributions is essentially _1_, and the logarithm of _1_ is _0_!
Even more important, the parts of every living thing are _communicating_ information - signaling - to other parts, near and far, as well as to other living things. Information communication allows each living thing to maintain itself in a state of _homeostasis_, balancing all matter and energy entering and leaving, maintaining all vital functions. Statistical physics and chemical thermodynamics know nothing of this biological information.