# The History of Quantum Physics The critical developments in quantum physics that are of greatest importance to information philosophy are not the works of the so-called "founders of quantum mechanics" in the late nineteen-twenties. Instead, they are the work of [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) between 1905 and 1917 that established the reality of atoms, discrete localized particles of matter, with his study of Brownian motion, but also _discrete particles_ of energy, light-quanta that are just as localized as matter is. In 1917 Einstein established the presence of irreducible [chance](https://www.informationphilosopher.com/chance/) in the universe, whenever matter and radiation interact. Quite apart from his great theories of special and general relativity, Einstein was one of the most important [creators](https://www.informationphilosopher.com/introduction/creation/) of quantum mechanics. His three 1905 papers on relativity, Brownian motion, and the light-quantum hypothesis (mischaracterized by many historians as the photo-electric effect, which was just one of three examples of light quanta), not only quantize the radiation field (Planck had only quantized the energy in his virtual oscillators), but they also show on a careful reading that Einstein was concerned about faster-than-light actions thirty years before his [Einstein-Podolsky-Rosen](https://www.informationphilosopher.com/solutions/experiments/EPR/) paper popularized the mysteries and paradoxes of quantum [nonlocality](https://www.informationphilosopher.com/problems/nonlocality/) and [entanglement](https://www.informationphilosopher.com/problems/entanglement/). Despite his foundational work quantizing radiation, Einstein rarely gets any credit for his contributions. There are a number of important reasons for this, which lead historians of quantum theory to start with Planck's quantum of action, then jump over Einstein's 1905 papers and his 1909 work on wave-particle duality to [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/)'s "old quantum theory" of the atom in 1913. Today, Bohr's "quantum jump" of an electron between stationary states is described as emitting or absorbing a "photon" of energy _hν_. In actuality, Bohr fought against Einstein's light-quantum hypothesis until the mid-1920's. Besides quantizing energy and seeing the interchangeability of radiation and matter, _E = mc2_, Einstein was the first scientist to see many of the most fundamental aspects of quantum physics, e.g., nonlocality and instantaneous action-at-a-distance (1905), wave-particle duality (1909), statistical elementary processes that introduce [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html) and [acausality](https://www.informationphilosopher.com/freedom/causality.html) whenever matter and radiation interact (1916-17), coherence, interference, and the indistinguishability of elementary particles (1925), and the non-separability and entanglement of interacting particles (1935). Ironically, and even tragically, Einstein could never accept most of his quantum discoveries, because they conflicted with his basic idea that nature is best described by a continuous field theory using differential equations that are functions of "local" variables, primarily the space-time four-vector of his general relativistic theory. Einstein's idea of a "local" reality is one where "action-at-a-distance" is limited to causal effects that propagate at or below the speed of light, according to his theory of relativity. Einstein's believed that quantum theory, as good as it is (and he saw nothing better), is "incomplete" because its statistical predictions (phenomenally accurate in the limit of large numbers of identical experiments - "ensembles" Einstein called them), tell us nothing about individual systems. Even worse, he thought that the wave functions of entangled systems predict faster-than-light correlations of properties between events in a space-like separation, violating his theory of relativity. This was the heart of his famous EPR paradox paper in 1935, but we shall see that Einstein was already concerned about faster-than-light transfer of energy in his earliest paper on quantum theory. The light-quantum hypothesis (1905) > Here Einstein first argues for a fundamental symmetry between matter and radiation. He does not yet mention that since _E = mc2_, energy and matter should be treated alike. > > A profound formal distinction exists between the theoretical concepts which physicists have formed regarding gases and other ponderable bodies and the Maxwellian theory of electromagnetic processes in so-called empty space. While we consider the state of a body to be completely determined by the positions and velocities of a very large, yet finite, number of atoms and electrons, we make use of continuous spatial functions to describe the electromagnetic state of a given volume, and a finite number of parameters cannot be regarded as sufficient for the complete determination of such a state. According to the Maxwellian theory, energy is to be considered a continuous spatial function in the case of all purely electromagnetic phenomena including light, while the energy of a ponderable object should, according to the present conceptions of physicists, be represented as a sum carried over the atoms and electrons.  > > How can energy spread continuously over a large volume later be absorbed in its entirety, without contradicting > his _principle of relativity_? > Einstein sees this, but does not say so explicitly until 1927. > > The energy of a ponderable body cannot be subdivided into arbitrarily many or arbitrarily small parts, while the energy of a beam of light from a point source (according to the Maxwellian theory of light or, more generally, according to any wave theory) is continuously spread over an ever increasing volume. > > The wave theory of light, which operates with continuous spatial functions, has worked well in the representation of purely optical phenomena and will probably never be replaced by another theory. It should be kept in mind, however, that the optical observations refer to time averages rather than instantaneous values. In spite of the complete experimental confirmation of the theory as applied to diffraction, reflection, refraction, dispersion, etc., it is still conceivable that the theory of light which operates with continuous spatial functions may lead to contradictions with experience when it is applied to the phenomena of emission and transformation of light. > > It seems to me that the observations associated with blackbody radiation, fluorescence, the production of cathode rays by ultraviolet light, and other related phenomena connected with the emission or transformation of light are more readily understood if one assumes that the energy of light is discontinuously distributed in space. > > In particular, the photoelectric effect showed discontinuous discrete light quanta, though it was doubted until the Compton Effect in 1923. > > In accordance with the assumption to be considered here, the energy of a light ray spreading out from a point source is not continuously distributed over an increasing space but consists of a finite number of energy quanta which are localized at points in space, which move without dividing, and which can only be produced and absorbed as complete units. > > We therefore arrive at the conclusion: the greater the energy density and the wavelength of a radiation, the more useful do the theoretical principles we have employed turn out to be; for small wavelengths and small radiation densities, however, these principles fail us completely. > > [W]e further conclude that: Monochromatic radiation of low density (within the range of validity of Wien's radiation formula) behaves thermodynamically as though it consisted of a number of independent energy quanta. > > Thermodynamically, radiation behaves like a gas. > Light cannot be spread out _continuously_ in all directions > if the energy is absorbed as a unit that ejects a photo-electron. > > [T]he energy of a light ray spreading out from a point source is not continuously distributed over an increasing space but consists of a finite number of energy quanta which are localized at points in space, which move without dividing, and which can only be produced and absorbed as complete units. > > The usual conception, that the energy of light is continuously distributed over the space through which it propagates, encounters very serious difficulties when one attempts to explain the photoelectric phenomena, > > Why did Bohr not see in 1913, or Einstein point out to him, that when an electron in an atom absorbs or emits energy, the jumping electron is accompanied by a single light quantum? > > According to the concept that the incident light consists of energy quanta..., however, one can conceive of the ejection of electrons by light in the following way. Energy quanta penetrate into the surface layer of the body, and their energy is transformed, at least in part, into kinetic energy of electrons. The simplest way to imagine this is that a light quantum delivers its entire energy to a single electron; we shall assume that this is what happens. > > > ("[A Heuristic Viewpoint on the Production and Transformation of Light](https://www.informationphilosopher.com/solutions/scientists/einstein/AJP_1905_photon.pdf)," English translation - _American Journal of Physics_, 33, 5, ) Wave-particle duality (1909) Einstein greatly expanded his light-quantum hypothesis in a presentation at the Salzburg conference in September, 1909. He argued that the interaction of radiation and matter involved elementary processes that are not _reversible_, a deep insight into the [irreversibility](https://www.informationphilosopher.com/quantum/history/problems/reversibility/) of natural processes. While incoming spherical waves of radiation are mathematically possible, they are not practically achievable. Nature appears to be [asymmetric in time](https://www.informationphilosopher.com/quantum/history/problems/arrow_of_time/). He speculates that the continuous electromagnetic field might be made up of large numbers of light quanta - singular points in the field that superimpose to create the wavelike behavior. Although he could not formulate a mathematical theory that does justice to both the oscillatory and quantum structures - the wave and particle pictures, Einstein argued that they are compatible over a decade before wave mechanics and quantum mechanics. And because gases behave statistically, he knows that the connection between wave and particles may involve [probabilistic](https://www.informationphilosopher.com/freedom/probability.html) behavior, which he will prove in 1916. > When light was shown to exhibit interference and diffraction, it seemed almost certain that light should be considered a wave. > > The greatest advance in theoretical optics since the introduction of the oscillation theory was Maxwell's brilliant discovery that light can be understood as an electromagnetic process...One became used to treating electric and magnetic fields as fundamental concepts that did not require a mechanical interpretation. > > This path leads to the so-called relativity theory. I only wish to bring in one of its consequences, for it brings with it certain modifications of the fundamental ideas of physics. It turns out that the inertial mass of an object decreases by L / c2 when that object emits radiation of energy L...the inertial mass of an object is diminished by the emission of light. > > Now Einstein looks for symmetry and equivalent treatment for interchangeable matter and energy. > > The energy given up was part of the mass of the object. One can further conclude that every absorption or release of energy brings with it an increase or decrease in the mass of the object under consideration. Energy and mass seem to be just as equivalent as heat and mechanical energy. > > Relativity theory has changed our views on light. Light is conceived not as a manifestation of the state of some hypothetical medium, but rather as an independent entity like matter. Moreover, this theory shares with the corpuscular theory of light the unusual property that light carries inertial mass from the emitting to the absorbing object. Relativity theory does not alter our conception of radiation's structure; in particular, it does not affect the distribution of energy in radiation-filled space. > > Einstein is about to tell us that the distribution of energy in radiation-filled space may be similar in some respects to the distribution of particles in matter-filled space! > > Nevertheless, with respect to this question, I believe that we stand at the beginning of a development of the greatest importance that cannot yet be surveyed. The statements that follow are largely my personal opinion, or the results of considerations that have not yet been checked enough by others. If I present them here in spite of their uncertainty, the reason is not an excessive faith in my own views, but rather the hope to induce one or another of you to deal with the questions considered. > > In the kinetic theory of molecules, for every process in which only a few elementary particles participate (e.g., molecular collisions), the inverse process also exists. But that is not the case for the elementary processes of radiation. > > Incoming spherical waves (the advanced potential considered by Wheeler and Feynman in 1945) are never observed in nature. Radiation is [irreversible](https://www.informationphilosopher.com/quantum/history/problems/reversibility/), one of the [arrows of time](https://www.informationphilosopher.com/quantum/history/problems/arrow_of_time/) > > According to our prevailing theory, an oscillating ion generates a spherical wave that propagates outwards. The inverse process does not exist as an elementary process. A converging spherical wave is mathematically possible, to be sure; but to approach its realization requires a vast number of emitting entities. The elementary process of emission is not invertible. In this, I believe, our oscillation theory does not hit the mark. Newton's emission theory of light seems to contain more truth with respect to this point than the oscillation theory since, first of all, the energy given to a light particle is not scattered over infinite space, but remains available for an elementary process of absorption. 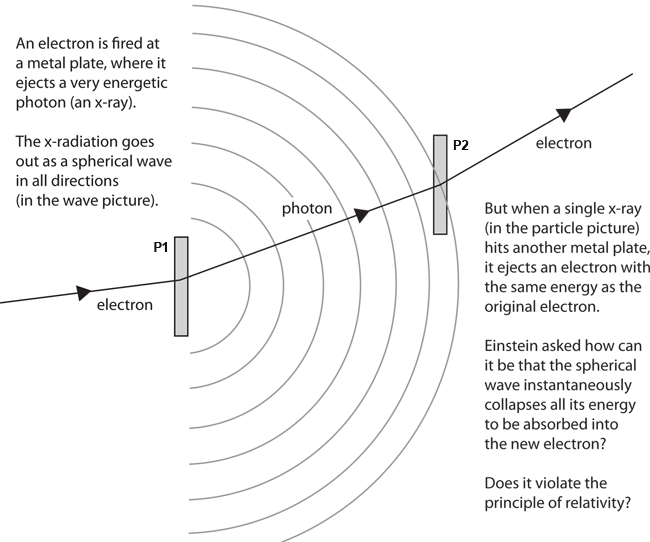> > Consider the laws governing the production of secondary cathode radiation by X-rays. If primary cathode rays impinge on a metal plate P1, they produce X-rays. If these X-rays impinge on a second metal plate P2, cathode rays are again produced whose speed is of the same order as that of the primary cathode rays. > >  > > As far as we know today, the speed of the secondary cathode rays depends neither on the distance between P1 and P2, nor on the intensity of the primary cathode rays, but rather entirely on the speed of the primary cathode rays. Let's assume that this is strictly true. What would happen if we reduced the intensity of the primary cathode rays or the size of P1 on which they fall, so that the impact of an electron of the primary cathode rays can be considered an isolated process? > > In his remarks after the talk, Johannes Stark confirmed that he had observed a single X-ray that traveled as far as ten meters and ejected a similar energy electron from P2. > > If the above is really true then, because of the independence of the secondary cathode rays' speed on the primary cathode rays' intensity, we must assume that an electron impinging on P1 will either cause no electrons to be produced at P2, or else a secondary emission of an electron whose speed is of the same order as that of the initial electron impinging on P1. In other words, the elementary process of radiation seems to occur in such a way that it does not scatter the energy of the primary electron in a spherical wave propagating in every direction, as the oscillation theory demands. > > That energy is possibly available "somewhere else" is the key idea of _nonlocality_ that Einstein will present in 1927 at the Solvay conference > > Rather, at least a large part of this energy seems to be available at some place on P2, or somewhere else. The elementary process of the emission of radiation appears to be directional. Moreover, one has the impression that the production of X-rays at P1 and the production of secondary cathode rays at P2 are essentially inverse processes. > > Therefore, the constitution of radiation seems to be different from what our oscillation theory predicts. The theory of thermal radiation has given important clues about this, mostly by the theory on which Planck based his radiation formula... > > Planck's theory leads to the following conjecture. If it is really true that a radiative resonator can only assume energy values that are multiples of _hν_, the obvious assumption is that the emission and absorption of light occurs only in these energy quantities. On the basis of this hypothesis, the light-quanta hypothesis, the questions raised above about the emission and absorption of light can be answered. As far as we know, the quantitative consequences of this light-quanta hypothesis are confirmed. This provokes the following question. Is it not thinkable that Planck's radiation formula is correct, but that another derivation could be found that does not rest on such a seemingly monstrous assumption as Planck's theory? Is it not possible to replace the light-quanta hypothesis with another assumption, with which one could do justice to known phenomena? If it is necessary to modify the theory's elements, couldn't one keep the propagation laws intact, and only change the conceptions of the elementary processes of emission and absorption? > > As far as I know, no mathematical theory has been advanced that does justice to both its oscillatory structure and its quantum structure... > > Anyway, this conception seems to me the most natural: that the manifestation of light's electromagnetic waves is constrained at singularity points, like the manifestation of electrostatic fields in the theory of the electron. It cannot be ruled out that, in such a theory, the entire energy of the electromagnetic field could be viewed as localized in these singularities, just like the old theory of action-at-a-distance. I imagine to myself, each such singular point surrounded by a field that has essentially the same character as a plane wave, and whose amplitude decreases with the distance between the singular points. If many such singularities are separated by a distance small with respect to the dimensions of the field of one singular point, their fields will be superimposed, and will form in their totality an oscillating field that is only slightly different from the oscillating field in our present electromagnetic theory of light. Of course, it need not be emphasized that such a picture is worthless unless it leads to an exact theory. I only wished to illustrate that the two structural properties of radiation according to Planck's formula (oscillation structure and quantum structure) should not be considered incompatible with one another. > > > ("[On the Development of Our Views Concerning the Nature and Constitution of Radiation](https://www.informationphilosopher.com/solutions/scientists/einstein/1909.html)," original in German, "Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung," _Physikalische Zeitschrift_, 10, 817-825, 1909 ) Perhaps the major reason for historians of quantum mechanics (writing since the [Copenhagen Interpretation](https://www.informationphilosopher.com/introduction/physics/copenhagen_interpretation.html)) to largely ignore Einstein is that he was the single most important _critic_ of the quantum mechanics formulated in the late 1920's by [Niels Bohr,](https://www.informationphilosopher.com/solutions/scientists/bohr/) [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/), [Max Born](https://www.informationphilosopher.com/solutions/scientists/born/), [Pascual Jordan](https://www.informationphilosopher.com/solutions/scientists/jordan/), [Wolfgang Pauli](https://www.informationphilosopher.com/solutions/scientists/pauli/), and [Paul DIrac](https://www.informationphilosopher.com/solutions/scientists/dirac/), whose work became the "standard orthodox" interpretation of quantum mechanics. So Einstein today is remembered more for his attacks than for his truly extraordinary fundamental contributions to quantum theory. Einstein's major objection was that quantum mechanics is a _statistical_ theory, one that predicts [probable](https://www.informationphilosopher.com/freedom/probability.html) results for a large number of experiments, but nothing about specific events, like the exact time of a radioactive decay or the direction of spontaneous emission of a photon. This "[chance](https://www.informationphilosopher.com/freedom/chance.html)" behavior of individual systems was something that Einstein himself pointed out in his early papers. But without the ability to predict individual events with certainty, he maintained that quantum mechanics must remain an _incomplete_ theory. Quantum mechanics can specify only as many physical variables as classical mechanics. Because of the [indeterminacy principle](https://www.informationphilosopher.com/freedom/indeterminacy.html), only one of each pair of non-commuting observables (momentum _or_ position, for example) can be specified precisely. In this sense, classical theory _is_ more complete. But rather than simply accept Einstein's description and terminology, Bohr, Heisenberg and others engaged in linguistic debates, claiming that quantum theory is itself "complete." They simply denied that more could be known about an underlying reality. A second concern for Einstein was that the wave function _ψ_ for an isolated free particle evolves in time to occupy all space. All positions become equally probable. Yet when we observe the particle, it is always located at some particular place. This does not prove that the particle had a particular place before the observation, but Einstein had a commitment to "elements of reality" that he thought no one could doubt. One of those elements is a particle's position. He asked the question, "Does the particle have a precise position the moment before it is measured?" The Copenhagen answer was sometimes "no," more often "don't know." If there is only one possible prior position for the particle, its path in four-dimensional space-time is fixed and determinate independently of the time. Complete path information is constant for all time. Quantum theory, by contrast, allows [alternative possibilities](https://www.informationphilosopher.com/freedom/possibilities.html) (with calculable [probabilities](https://www.informationphilosopher.com/freedom/probability.html)) that are critical if there is to be more than one possible future. ## The Old Quantum Theory The so-called "old" quantum theory began at the turn of the twentieth century when Max Planck assumed that a physical property called action, the product of momentum and position (or of energy and time) was not a _continuous_ variable, but comes in _discrete_ packets he called _h_, the "quantum of action." It was just a year after J. J. Thomson had discovered the electron as a material particle and [Ludwig Boltzmann](https://www.informationphilosopher.com/solutions/scientists/boltzmann/)'s insight into the statistical mechanics of atoms was starting to find acceptance by most physicists. Planck considered his assumption merely a mathematical hypothesis needed to make his theoretical formula for the distribution of _continuous_ electromagnetic radiation correspond to experimental evidence. He did not believe in the reality of _discrete_ energy quanta for many years, if he ever accepted them fully. It is curious that the first assumption of discreteness came from the theory of the continuous spectrum of electromagnetic waves, because the first hints of discreteness, and even the first appearance of quantum numbers as integers came from the study of spectral lines in the nineteenth century. Of course the chemists of the early nineteenth century assigned integers to atoms based on the discrete ratios of combinations with other atoms, H2O and CaCl2, for example.