# Disentanglement and the Bell Inequalities In the year following the [Einstein-Podsky-Rosen](https://www.informationphilosopher.com/solutions/experiments/EPR/) paper, [Erwin Schrödinger](https://www.informationphilosopher.com/solutions/scientist/schrodinger/) looked more carefully at [Einstein](https://www.informationphilosopher.com/solutions/scientist/einstein/)'s "separability" assumption (_Trennungsprinzip_) that an entangled system can be separated enough to be regarded as two systems with independent wave functions: > Years ago I pointed out that when two systems separate far enough to make it possible to experiment on one of them without interfering with the other, they are bound to pass, during the process of separation, through stages which were beyond the range of quantum mechanics as it stood then. For it seems hard to imagine a complete separation, whilst the systems are still so close to each other, that, from the classical point of view, their interaction could still be described as an unretarded _actio in distans_. And ordinary quantum mechanics, on account of its thoroughly unrelativistic character, really only deals with the _actio in distans_ case. The whole system (comprising in our case both systems) has to be small enough to be able to neglect the time that light takes to travel across the system, compared with such periods of the system as are essentially involved in the changes that take place... > > It seems worth noticing that the paradox could be avoided by a very simple assumption, namely if the situation after separating were described by the expansion > [_ψ (x,y) = Σ ak gk(x) fk(y)_, > as assumed in EPR], but with the additional statement that the knowledge of the phase relations between the complex constants ak has been entirely lost in consequence of the process of separation. > > When some interaction, like a measurement, causes a _separation_, the two-particle wave function Ψ12 collapses, the system decoheres into the product Ψ1Ψ2, losing their "influence" on one another, but not the acquisition of information about the second system by (nonlocal) measurements on the first. > > This would mean that not only the parts, but the whole system, would be in the situation of a mixture, not of a pure state. It would not preclude the possibility of determining the state of the first system by suitable measurements in the second one or vice versa. But it would utterly eliminate the experimenters influence on the state of that system which he does not touch. > > > ("[Probability Relations between Separated Systems](https://www.informationphilosopher.com/solutions/scientist/schrodinger/Schrodinger-1936.pdf)," _Proceedings of the Cambridge Physical Society_ 1936, 32, issue 2, p.446-452) Schrödinger says that the entangled system may become disentangled (Einstein's separation) and yet some perfect correlations between later measurements might remain. Note that the entangled system could simply decohere as a result of interactions with the environment, as proposed by [decoherence](https://www.informationphilosopher.com/quantum/decoherence/) theorists. The perfectly correlated results of [Bell-inequality](https://www.informationphilosopher.com/quantum/bell_theorem/) experiments might nevertheless be preserved, depending on the interaction. Schrödinger tells us that the two-particle wave function Ψ12 will be separated into the product of single-particle wave functions Ψ1 and Ψ2 by a measurement of either particle, for example, by either Alice's or Bob's measurements in the case of Bell's Theorem. ## Bell's Theorem Following [David Bohm](https://www.informationphilosopher.com/solutions/scientist/bohm/)'s version of EPR, [John Bell](https://www.informationphilosopher.com/solutions/scientist/bell/) considered two spin-1/2 particles in an entangled state with total spin zero. | ψ > = (1/√2) | + - > - (1/√2) | - + >       (1) This is a superposition of two states, either of which conserves total spin zero. The minus sign ensures the state is anti-symmetric, changing sign under interchange of identical electrons. The coefficients 1/√2, when squared, give us the 1/2 probability of finding either state. Schrödinger does not mention _conservation principles_, but he knows that [EPR](https://www.informationphilosopher.com/solutions/experiments/EPR/) used them to gather [knowledge](https://www.informationphilosopher.com/knowledge/) about the second system by measurements on the first, as he accepts. Conservation principles are the deep reason for the perfect correlations between various observables, i.e., conservation of mass, energy, momentum, angular momentum, and in Bell's case spin. Let's assume that Alice makes a measurement of a spin component of one particle, say the x-component. First, her measurement projects the entangled system randomly into either the | + - > or | - + > state. Alice measures + (spin up) or - (spin down). A succession of such random outcomes produces the bit string with "true randomness" (Gisin, 2014) or "really random" and "totally random" (Bub, 2016, 2018) that is needed for use as a quantum key code in quantum cryptography. If Alice measures the x-component and finds spin up, equation 1 becomes | ψ > = | + - >       (2) Using Schrödinger's expansion of the two-particle wave function in products of single-particle wave functions, we can further write | ψ > = | + >x | - >x       (3) Schrödinger describes the entangled system as having separated, _disentangled_ into the product of independent single-particle wave functions | + >x and | - >x. The two particles continue to evolve apart. But now we can say that future measurements of Alice's particle are _determined_ to be found with the x-component of spin up (| + >x), and the x-component of Bob's particle spin down (| - >x), by conservation of angular momentum. But Bob will find his particle spin down with certainty _if and only if_ he measures at the same angle as Alice. If Bob measures at any other angle, the perfect anti-correlation that distributes perfectly matched quantum key pairs to Alice and Bob will be lost. Bell's inequality was a study of how these perfect correlations decrease as a function of the angle between measurements by Alice and Bob. Bell predicted local hidden variables would produce a _linear_ function of this angle, whereas, he said, quantum mechanics should produce a dependence on the cosine of this angle. As the angle changes, admixtures of other states will be found, for example | + + > in which Alice and Bob both measure spin up. Bell wrote that "Since we can predict in advance the result of measuring any chosen component of **σ**2, by previously measuring the same component of **σ**1, it follows that the result of any such measurement must actually be predetermined." [David Bohm](https://www.informationphilosopher.com/solutions/scientist/bohm/) has shown that these values were not predetermined (they did not even exist according to the [Copenhagen Interpretation](https://www.informationphilosopher.com/quantum/copenhagen/)) _before_ Alice's measurement. According to [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientist/heisenberg/) and [Pascual Jordan](https://www.informationphilosopher.com/solutions/scientist/jordan/), Alice's x-component of spin is _created_ by Alice's measurement in the x-direction, the result of Alice's "[free choice](https://www.informationphilosopher.com/freedom/free_choice.html)." According to [Paul Dirac](https://www.informationphilosopher.com/solutions/scientist/dirac/), Alice's _random_ x-component value depends on "Nature's choice," the source of what Nicolas Gisin (2014) calls the "true randomness" needed for quantum key distribution. Many commentators on Bell's theorem claim that Alice and Bob's spin component values can not pre-exist their measurements, certainly not (as Bohm showed) from their initial preparation in the total spin-zero entangled state (1). In that case, spin component values would have to pre-exist in all three dimensions, they say. In his landmark 1985 article "Is the moon there when nobody looks? Reality and the quantum theory," [David Mermin](https://www.informationphilosopher.com/solutions/scientist/mermin/) wrote "it [pre-existing spins] amounts to the insistence that each particle has stamped on it in advance the outcome of the measurements of three different spin components corresponding to noncommuting observables **S·a(i)**, i = l,2, 3." But Bohm showed that the single spin component in the x-direction is _created_ when Alice measures the two-particle wave function _ψ12_ in the x-direction. Alice's measurement collapses _ψ12_ and disentangles/decoheres it into Schrödinger's product of single-particle wave functions, _ψ1x_ and _ψ2x_ ( | + >x and | - >x ). The nonlocal collapse of the two-particle wave function _conserves_ the total spin zero, so that Bob's now-independent x-component of spin is precisely opposite to that of Alice. And it is that same spin x-component that Bob must measure to get the perfect anti-correlations needed for quantum cryptography keys. The other two (unmeasured) spin components have no definite values. They are still in random superpositions (their overall rotational symmetry still ensuring conservation of angular momentum). Indeed, should Bob measure a different angle from Alice, we get the angle-dependent results of the Bell inequalities. Bell predicted a _linear_ fall-off for _local_ hidden variables and a cosine dependence for quantum mechanics. But every experiment has confirmed the quantum mechanical dependence on the cosine of the angle between Alice's and Bob's measurements. The cosine squared dependence of the intensity of light passing through crossed polarizers was discovered in 1809 by Étienne Louis Malus. It is known as the "law of Malus." In the important case where Alice and Bob measure at the same angle, the cosine of zero is 1 and the correlation is perfect. This corresponds to [Paul Dirac](https://www.informationphilosopher.com/solutions/scientist/dirac/)'s assertion that there are some cases where quantum mechanical experiments involve no [indeterminism](https://www.informationphilosopher.com/freedom/indeterminacy.html). Dirac mentions the case of measuring a photon passing through a vertical polarizer that has been prepared in a vertical state of polarization. The probability is unity or certainty, Dirac says. > Only when the initial state and the observation are such that there is a probability unity, i.e. a certainty, for one particular result is it possible that the observation may produce no change of state... > > The state of a system after a maximum observation has been made on it is such that there exists a maximum observation (namely, an immediate repetition of the maximum observation already made) which, when made on the system in this state, will for a certainty lead to one particular result (namely, the previous result over again). > > > _The Principles of Quantum Mechanics_, Chapter 1, p.16, 1930 This is the origin of the [quantum Zeno effect](https://en.wikipedia.org/wiki/Quantum_Zeno_effect). We can visualize the angles in the Bell experiments that correspond to measuring the same angles, or directly opposite angles, which according to Dirac give equally certain outcomes. We can also show Bell's straight-line predictions for local hidden variables, the sides of the square of the local hidden variables "polytope." The certain outcomes are at the corners of the square, 0°, 90°, 180°, 270°, where Bell somewhat unrealistically predicted there would be "kinks" instead of the smooth curvature of the cosines at the corners that are predicted by quantum mechanics.  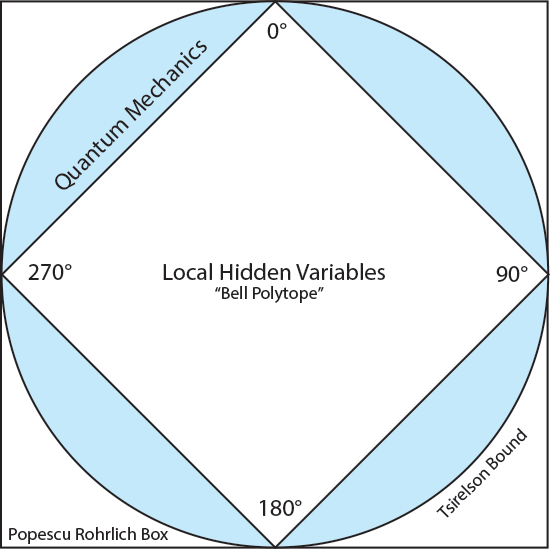This figure shows the straight-line predictions of Bell's inequalities for local hidden variables, the cosine curves predicted by quantum mechanics and conservation of angular momentum, and the odd "kinks" at angles 0°, 90°, 180°, and 270°, in what may be called a "Popescu-Rorhlich box." The "PR Box" shows Bell’s local hidden variables prediction as four straight lines of the inner square. The circular region of quantum mechanics correlations are found outside Bell's straight lines, "violating" his inequalities. 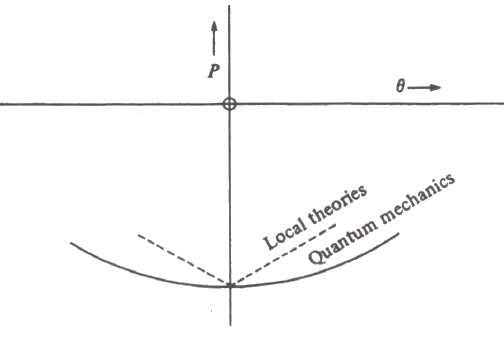Quantum mechanics and Bell's inequalities meet at the corners, where Bell's predictions show a distinctly non-physical right-angle that Bell called a "kink." All experimental results have been found to lie along the curved quantum predictions called the "Tsirelson bound." (Tsirelson, 1980)  In 1976, Bell gave us this diagram of the "kinks" in his local hidden variables inequality. He says, > Unlike the quantum correlation, which is stationary in _θ_ at _θ = 0_, at the hidden variable correlation must have a kink there. > > > ("Einstein-Podolsky-Rosen Experiments," republished in _Speakable and Unspeakable in Quantum Mechanics,_" 1987, p. 85) ## Violating Tsirelson's Bound?  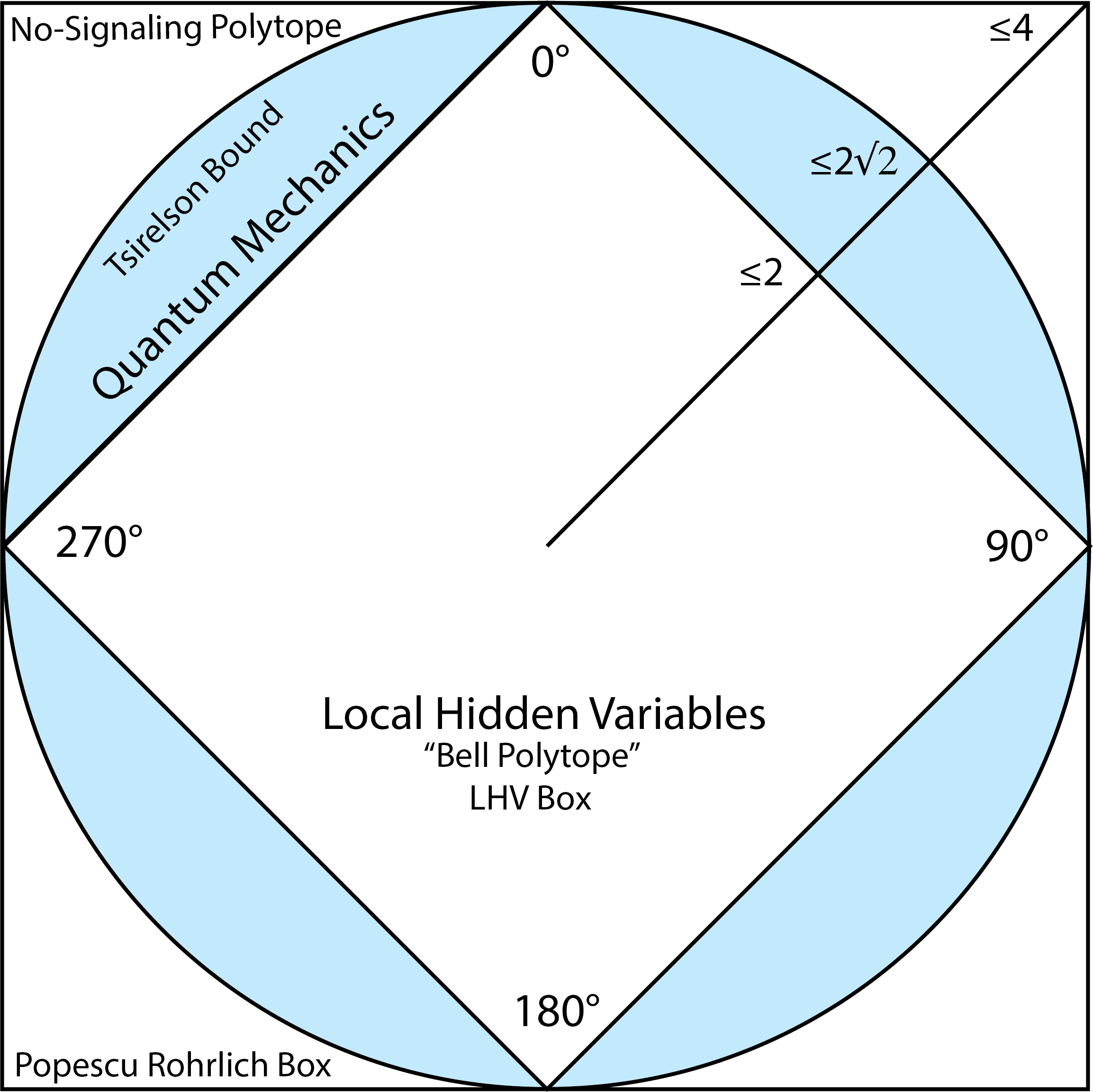In 1994, Sandu Popescu and Daniel Rohrlich proposed two new axioms of quantum mechanics, _relativistic causality_ and _nonlocality_. Relativity limits _causality_ to "light cones," inside which events can signal one another without exceeding light speed. Nonlocality involves events outside one another's light cones, where no signaling is possible. Popescu and Rohrlich proposed that entangled Bell states might exhibit nonlocal correlations even beyond Tsirelson's bound, a theory they called "superquantum mechanics," one more nonlocal than quantum theory. They would not only violate Bell's inequalities but also violate quantum mechanics, by going beyond Tsirelson's bound. These hypothetical nonlocal correlations, found in the outermost square, would violate quantum mechanics but not the principle of relativity, because there is no signaling. Whereas Bell's inequalities predict the sum of correlations is ≤2 for local hidden variables, and quantum mechanics predicts ≤2√2, "superquantum" correlations are ≤4. Popescu and Rohrlich asked "Where does this bound come from? It derives from the Hilbert space structure of quantum mechanics, but what does it mean?" (1994, p.382) One answer comes from C.S. Unnikrishnan (2005), > "The correlation function allowed by the basic assumption of validity of conservation law is unique, and surprisingly it is identical to the quantum mechanical correlation function. Therefore, a physical system with discrete observable values can show correlations different from what is predicted by quantum mechanics only by violating a fundamental conservation law" > > > (""Correlation functions. Bell's inequalities and the fundamental conservation laws." _Europhys. Lett._ 69, 489-495, 2005) The perfect correlations of entangled spin states are the result of the conservation of total electron spin zero. The fall-off in correlations when Alice and Bob measure at different angles is a consequence of the "law of Malus." ## Popescu-Rohrlich Boxes In classic Bell experiments, Alice and Bob make a series of measurements with outcomes that can be described with binary numbers, (1,0) = | + >|- >, (0,1) = | - >| + >, (1,1) = | +>| + >, (0,0) = | - >| - >. They count the numbers of different outcomes and relate them to the probabilities of those outcomes, _P(a,b|x,y)_, where x,y = ±1. In the jargon of quantum nonlocality, _P(a,b|x,y)_ is called a "box," because the correlation probabilities might be built into a physical box with inputs x,y = ±1 and outputs a,b = ±1. Compare [David Mermin](https://www.informationphilosopher.com/solutions/scientist/mermin/)'s devices. ||_x = 0_|_x = 1_| |---|---|---| |_y = 0_|_a = b_|_a = b_| |_y = 1_|_a = b_|_a ≠ b_| Nicolas Gisin (2014, p.13) and Jeffrey Bub (2016, p.89) both describe their boxes as describable by a simple equation a **+** b = x**·**y where the addition operation **+** is modulo 2. ## Decoherence and Disentanglement? Might [decoherence](https://www.informationphilosopher.com/quantum/decoherence/) by environmental interactions _cause_ the superposition of states | + - > - | - + > (equation 3) to collapse into one of these states and then into a product of single particle states, as Schrödinger told Einstein would happen for disentanglement? And does this also lead to the _appearance_ of nonlocal simultaneous events, events that conserve angular momentum, in spatial regions where no-signaling applies? If so, conservation of angular momentum is all that is necessary for perfectly correlated quantum key distribution via entangled Bell states, without any "spooky action-at-a-distance," without any "influence" of one particle on the other at faster-than light speeds, just as Schrödinger thought in 1936. Alice's "first" measurement of a spin x-component would still be the "cause" of Bob's perfect correlation (assuming Bob measures in the same x-direction, of course). Correlations would be because the two spins were in a superposition of perfectly opposed directions before Alice's measurement, both conserving angular momentum. (Unnikrishnan, 2005) According to Asher Peres (1998), [Nathan Rosen in 1931](https://www.informationphilosopher.com/solutions/scientist/bell/Rosen_H2.pdf) described the normal hydrogen molecule with a two-particle wave function that he years later recognized was a Schrödinger "entangled state." Rosen wrote _ψ = ψ(al)ψ(b2) + ψ(b1)ψ(a2)_. ## Can Perfect Correlations Be Explained by Conservation Laws? [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/), [Eugene Wigner](https://www.informationphilosopher.com/solutions/scientists/wigner/), and even [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) suggested that _conservation of angular momentum_ (or particle spin) tells us that if one spin-1/2 electron is measured up, the other must be down. [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) used conservation of _linear_ momentum in his development of the [EPR Paradox](https://www.informationphilosopher.com/solutions/experiments/EPR/). Bohm changed from the _continuous_ variables position and momentum to the _discrete_ quantum variable of electron spin. Bohm wrote in his 1952 book _Quantum Theory_, "We shall now describe the hypothetical experiment of Einstein, Rosen, and Podolsky. We have modified the experiment somewhat, but the form is conceptually equivalent to that suggested by them, and considerably easier to treat mathematically." > The system containing the spin of two atoms has four basic wave functions, from which an arbitrary wave function can be constructed. > These are > > _ψa = u+(1)u+(2)_ > _ψa = u-(1)u-(2)_ > _ψa = u+(1)u-(2)_ > _ψa = u-(1)u+(2)_ > > where u+ and u- are the one-particle spin wave functions representing, respectively, a spin ℏ/2 and -ℏ/2, and the argument (1) or (2) refers, respectively, to the particle which has this spin. Now ψc and ψd represent the two possible situations in which each particle has a definite z component of the spin in a direction which is opposite to that of the other. The wave function for a system of total spin zero is the following linear combination of ψc - ψd and ψc - ψd. > > _ψ0 = 1/√2(ψc - ψd)_ > > > "The Hypothetical Experiment of Einstein, Rosen, and Podolsky," in _Quantum Theory_ pp. 615-616 > [Because the wave function] has definite phase relations between ψc and ψd, the system must cover the states corresponding to ψc and ψd simultaneously. Thus, for a given atom, no component of the spin of a given variable exists with a precisely defined value, until interaction with a suitable system, such as a measuring apparatus, has taken place. But as soon as either atom (say, No. 1) interacts with an apparatus measuring a given component of the spin, definite phase relations between ψc and ψd are destroyed. This means that the system then acts as if it is either in the state ψc or ψd. Thus, in every instance in which particle No. 1 develops a definite spin component in, for example, the z direction, the wave function of particle No. 2 will automatically take such a form that it guarantees the development of the opposite value of σz if this particle also interacts with an apparatus which measures the same component of the spin. The wave function therefore describes the propagation of correlated potentialities. Because the expansion of the wave function ψ0 takes the same form when expanded in terms of the eigenfunctions of an arbitrary component of the spin, we conclude that similar correlations will be obtained if the same component of the spin of each atom in any direction is measured. Moreover, because the potentialities for development of a definite spin component are not realized irrevocably until interaction with the apparatus actually takes place, there is no inconsistency in the statement that while the atoms are still in flight, one can rotate the apparatus into an arbitrary direction, and thus choose to develop definite and correlated values for any desired spin component of each atom. > > > "The Hypothetical Experiment of Einstein, Rosen, and Podolsky," in _Quantum Theory_ pp. 621-622 Bohm explained that in classical theory, the spin correlations are produced because when the atoms of the original molecule separated, each atom would continue to have every component of its spin angular momentum opposite to that of the other. He says this is _conservation_ of the spin-angular-momentum for each component of the separate vectors. In quantum mechanics, however, the investigator can measure either the x, y, or z component of the spin of a particle, but not more than one of these components, in any one experiment. Nevertheless, it still turns out that whichever component of particle 1 is measured, the results are correlated, so that if the same component of particle 2 is measured, it will always turn out to have the opposite value. He writes > Now, if the spin were a classical angular momentum variable, the interpretation of this process would be as follows: While the two atoms were together in the form of a molecule, each component of the angular momentum of each atom would have a definite value that was always opposite to that of the other, thus making the total angular momentum equal to zero. When the atoms separated, each atom would continue to have every component of its spin angular momentum opposite to that of the other. The two spin-angular-momentum vectors would therefore be correlated. These correlations were originally produced when the atoms interacted in such a way as to form a molecule of zero total spin, but after the atoms separate, the correlations are maintained by the deterministic equations of motion of each spin vector separately, which bring about conservation of each component of the separate spin-angular- momentum vectors. > > Suppose now that one measures the spin angular momentum of any one of the particles, say No. 1. Because of the existence of correlations, one can immediately conclude that the angular-momentum vector of the other particle (No. 2) is equal and opposite to that of No. 1. In this way, one can measure the angular momentum of particle No. 2 indirectly by measuring the corresponding vector of particle No. 1. > > Let us now consider how this experiment is to be described in the quantum theory. Here, the investigator can measure either the x, y, or z component of the spin of particle No. 1, but not more than one of these components, in any one experiment. Nevertheless, it still turns out as we shall see that whichever component is measured, the results are correlated, so that if the same component of the spin of atom No. 2 is measured, it will always turn out to have the opposite value. This means that a measurement of any component of the spin of atom No. 1 provides, as in classical theory, an indirect measurement of the same component of the spin of atom No. 2. Since, by hypothesis, the two particles no longer interact, we have obtained a way of measuring an arbitrary component of the spin of particle No. 2 without in any way disturbing that particle. > > > _ibid_ pp. 614-615 With his colleague, Yakir Aharonov, in 1957 Bohm reiterated his model > We consider a molecule of total spin zero consisting of two atoms, each of spin one-half. The wave function of the system is therefore > > _ψ_ = (1/√2) [ _ψ+ (1) ψ- (2) - ψ- (1) ψ+ (2)_ ] > > where ψ_+_ (1) refers to the wave function of the atomic state in which one particle (A) has spin +ℏ/2, etc. The two atoms are then separated by a method that does not influence the total spin. After they have separated enough so that they cease to interact, any desired component of the spin of the first particle (A) is measured. Then, because the total spin is still zero, it can immediately be concluded that the same component of the spin of the other particle (B) is opposite to that of A. > > > "Discussion of Experimental Proof for the Paradox of Einstein, Rosen, and Podolsky,” _Physical Review_, vol.108, no.4. p.1070, 1957 [Eugene Wigner](https://www.informationphilosopher.com/solutions/scientists/wigner/) wrote in 1962 Writing a few years after Bohm, and one year before Bell, Wigner explicitly describes Einstein's work with the conservation of linear momentum as well as Bohm's conservation of angular momentum (spin) that explains perfect correlations between angular momentum (spin) components measured in the same direction > If a measurement of the momentum of one of the particles is carried out — the possibility of this is never questioned — and gives the result **p**, the state vector of the other particle suddenly becomes a (slightly damped) plane wave with the momentum -**p**. This statement is synonymous with the statement that a measurement of the momentum of the second particle would give the result -**p**, as follows from the conservation law for linear momentum. The same conclusion can be arrived at also by a formal calculation of the possible results of a joint measurement of the momenta of the two particles. > > One can go even further: instead of measuring the linear momentum of one particle, one can measure its angular momentum about a fixed axis. If this measurement yields the value _mℏ_, the state vector of the other particle suddenly becomes a cylindrical wave for which the same component of the angular momentum is -_mℏ_. This statement is again synonymous with the statement that a measurement of the said component of the angular momentum of the second particle certainly would give the value -_mℏ_. This can be inferred again from the conservation law of the angular momentum (which is zero for the two particles together) or by means of a formal analysis. > > (_The Problem of Measurement_, Eugene Wigner, in Wheeler and Zurek, p,340) [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) wrote in 1964, > With the example advocated by Bohm and Aharonov, the EPR argument is the following. Consider a pair of spin one-half particles formed somehow in the singlet spin state and moving freely in opposite directions. Measurements can be made, say by Stern-Gerlach magnets, on selected components of the spins **σ**1 and **σ**2. If measurement of the component **σ**1 • **a**, where **a** is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of **σ**2 • **a** must yield the value — 1 and vice versa. Now we make the hypothesis, and it seems one at least worth considering, that if the two measurements are made at places remote from one another the orientation of one magnet does not influence the result obtained with the other.  > > "[pre-determination](https://www.informationphilosopher.com/freedom/pre-determinism.html)" is too strong a term. The first measurement just "determines" the later measurement. We shall see that the second measurement is synchronous with the "first" in a "special" frame > > Since we can predict in advance the result of measuring any chosen component of **σ**2, by previously measuring the same component of **σ**1, it follows that the result of any such measurement must actually be predetermined. > > Since the initial quantum mechanical wave function does not determine the result of an individual measurement, this predetermination implies the possibility of a more complete specification of the state. > > > ("[On the Einstein-Podolsky-Rosen Paradox](https://www.informationphilosopher.com/quantum/disentanglement/Bell_On_EPR.pdf)," _Physics_, 1.3, p.195.) Where Bohm and Wigner are explicit, Bell is _implicitly_ using the conservation of total spin. [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) made the same implicit argument in 1933, shortly before [EPR](https://www.informationphilosopher.com/knowledge/ERR/), though again with conservation of _linear momentum_, asking Leon Rosenfeld, > Suppose two particles are set in motion towards each other with the same, very large, momentum, and they interact with each other for a very short time when they pass at known positions. Consider now an observer who gets hold of one of the particles, far away from the region of interaction, and measures its momentum: then, from the conditions of the experiment, he will obviously be able to deduce the momentum of the other particle. If, however, he chooses to measure the position of the first particle, he will be able tell where the other particle is. > > > (_Niels Bohr, His Life and Work as seen by His Friends and Colleagues_, 1967, S. Rozental, pp.128-129) Supporters of the [Copenhagen Interpretation](https://www.informationphilosopher.com/quantum/copenhagen/) claim that the properties of the particles (like angular or linear momentum) _do not exist_ until they are measured. It was [Pascual Jordan](https://www.informationphilosopher.com/solutions/scientists/jordan/) who claimed the measurement _creates_ the value of a property. This is true when the preparation of the state is in an unknown linear combination (_superposition_) of quantum states. In our case, the entangled particles have been prepared in a superposition of [Bell] states, both of which have total spin zero. _ψ12_ = (1/√2) [ _ψ+ (1) ψ- (2) - ψ- (1) ψ+ (2)_] So whichever of these two states is _projected_ by a later measurement or decoherence, it will put the two particles in opposite spin states, randomly + - or - + , but still supporting the views of Bohm, Wigner, and Bell, that they will be perfectly (anti-)correlated when measured, because of conservation of angular momentum (spin). Einstein famously maintained that the strongest theories are those built on universal principles. Surely conservation principles, which [Emmy Noether](https://www.informationphilosopher.com/solutions/scientists/noether) showed are built on the still deeper and simpler concept of symmetry, should be a part of any basis for physics, classical or quantum. ## Conclusion As [Emmy Noether](https://www.informationphilosopher.com/solutions/scientists/noether/) showed, conservation laws arise from deeper principles of symmetry. The perfect symmetry between the indistinguishable electrons in Bohm's entanglement experiment, the perfect symmetry of their two-particle wave function, and the change of sign of that wave function under exchange of the two identical particles, all are evidence of _synchronous_ events that are not directional "influences" of one on the other (not Einstein's "spooky action-at-a-distance"). They are _simultaneous_ events in a "special frame" in which their center of mass is static. These events _conserve_ the rotationally symmetric total spin zero at the same moment the two particles are disentangled and can no longer be described with a two-particle wave function. They are now described by the product of two single-particle wave functions. The original pure state superposition has decohered. They are now _disentangled_ and in a mixed state. As Schrödinger wrote, "knowledge of the phase relations between the complex constants ak has been entirely lost in consequence of the process of separation." The symmetry and angular momentum conservation of entangled particles is theoretically deeper than classical and quantum physics. The theory of entanglement is confirmed by all experiments that measure spins in exactly the same direction, as Bohm, Bell, and Wigner all agree. Unlike most quantum experiments, the results are not a statistical distribution around some expectation value. Conservation is deeper than quantum mechanics. This entanglement is the basis for generation of _random_ bit sequences at distant locations, which when compared are perfectly (anti-)correlated and usable as distributed quantum keys for securely encrypted communications. It is also the basis for the instantaneous "teleportation" of quantum information. Conservation is not a _causal_ "force" by which one particle "acts" on the other, as Einstein feared. But it can explain the strange connection between widely separated events that he saw as "nonlocality," perhaps as early as 1905, explicitly described at the [Solvay conference in 1927](https://www.informationphilosopher.com/solutions/scientists/einstein/#solvay5), and made famous in his 1935 [EPR paper](https://www.informationphilosopher.com/solutions/experiments/EPR/). ## References Alcock, J., Brunner, N., Pawlowski, M., and Scarani, V. (2009) "Recovering part of the quantum boundary from information causality," [arxiv.org/0906.3464](https://arxiv.org/pdf/0906.3464.pdf) Bell, J., (1964) "On the Einstein Podolsky Rosen Paradox." _Physics_ 1.3 195. [aps.org](https://link.aps.org/pdf/10.1103/PhysicsPhysiqueFizika.1.195) Bub, J., (2004) "Why the Quantum?" _Stud. Hist. Philos. Modern Phys._ 35B, 241-266. [arxiv.org/0402149](https://arxiv.org/pdf/0402149) ________, (2012) "Why the Tsirelson bound?," in _Probability in Physics_. Springer, Berlin, Heidelberg, 167-185. [arxiv.org/1208.3744](https://arxiv.org/pdf/1208.3744.pdf) ________, (2016) _Bananaworld: Quantum Mechanics for Primates_. Oxford University Press. ________, (2018) _Totally Random: why nobody understands quantum mechanics (a serious comic on entanglement)._. Princeton University Press. Gisin, N., (2014) _Quantum Chance: Nonlocality, Teleportation, and other Quantum Marvels_, Springer. Mermin, D. (1985) "Is the moon there when nobody looks? Reality and the quantum theory," _Physics Today_ 38.4 38-47 [informationphilosopher.com](https://www.informationphilosopher.com/solutions/scientist/bell/Mermin_Phys.Today.38.38.pdf) Pawłowski, M., Paterek, T., Kaszlikowski, D., Scarani, V., Winter, A., & Żukowski, M. (2009) "Information causality as a physical principle." _Nature_, 461(7267), 1101-1104. [arxiv.org/0905.2292](https://arxiv.org/pdf/0905.2292) Peres, Asher. (1998) "Quantum disentanglement and computation." _Superlattices and Microstructures_ 23.3-4, 373-379. [arxiv.org/9707047](https://arxiv.org/pdf/quant-ph/9707047) Popescu, S., and Rohrlich, D. (1994) "Quantum nonlocality as an axiom." _Foundations of Physics_ 24.3, 379-385. [informationphilosopher.com](https://www.informationphilosopher.com/solutions/scientist/bell/Popescu_Rohrlich.pdf) Rosen, N. (1931) "The normal state of the hydrogen molecule." _Physical Review_ 38.12 2099. [informationphilosopher.com](https://www.informationphilosopher.com/solutions/scientist/bell/Rosen_H2.pdf) Schrödinger, E. (1936) "Probability Relations between Separated Systems," _Proceedings of the Cambridge Physical Society_ 32, issue 2, p.446-452 [informationphilosopher.com](https://www.informationphilosopher.com/solutions/scientist/schrodinger/Schrodinger-1936.pdf) Stuckey, W, Silberstein, M, McDevitt, T. and Kohler, I. (2019) "Why the Tsirelson bound? Bub’s question and Fuchs’ desideratum." _Entropy_ 21.7, 692. [mdpi.com](https://www.mdpi.com/1099-4300/21/7/692/pdf) Stuckey, W, Silberstein, M, McDevitt, T. and Le, T.D. (2020) "Answering Mermin’s Challenge with Conservation per No Preferred Reference Frame." [researchgate.net](https://www.researchgate.net/profile/Mark_Stuckey/publication/327858970_Quantum_Mysteries_for_Anybody_Solved/links/5ec70aea458515626cbf2e40/Quantum-Mysteries-for-Anybody-Solved.pdf) Tsirelson, B.S. (1980) "Quantum Generalizations of Bell's Inequality." _Lett. Math. Phys._ 4, 93-100, [informationphilosopher.com](https://www.informationphilosopher.com/solutions/scientist/bell/Tsirelson.pdf) Unnikrishnan, C.S. (2005) "Correlation functions. Bell's inequalities and the fundamental conservation laws." _Europhys. Lett._ 69, 489-495. [arxiv.org/0407041](https://arxiv.org/pdf/quant-ph/0407041) [ ](https://www.informationphilosopher.com/quantum/disentanglement/)