# Einstein-Podolsky-Rosen Like the [Schrödinger's Cat](https://www.informationphilosopher.com/solutions/experiments/schrodingerscat/) paradox, the 1935 thought experiment proposed by [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/), [Boris Podolsky](http://en.wikipedia.org/wiki/Boris_Podolsky), and [Nathan Rosen](http://en.wikipedia.org/wiki/Nathan_Rosen) (and known by their initials as EPR), was originally proposed to exhibit internal contradictions in the new quantum physics. Einstein hoped to show that quantum theory could not describe certain intuitive "elements of reality" and thus was either _incomplete_ or, as he may have hoped, demonstrably incorrect. Einstein was correct that quantum theory is "_incomplete_" relative to classical physics, which has twice as many dynamical variables that can be known with arbitrary precision. But half of this information is missing in quantum physics, making it statistical. [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/)'s [indeterminacy (or uncertainty) principle](https://www.informationphilosopher.com/freedom/indeterminacy.html) allows only one of each pair of non-commuting observables (for example momentum _or_ position) to be known with arbitrary accuracy. Einstein and his colleagues [Erwin Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/), [Max Planck](https://www.informationphilosopher.com/solutions/scientists/planck/), and [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/), initially hoped for a return to [deterministic](https://www.informationphilosopher.com/freedom/determinism.html) physics, and the elimination of mysterious phenomena like the [_superposition of states_](https://www.informationphilosopher.com/solutions/experiments/dirac_three-polarizers/) and the ["collapse" of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). EPR continues to fascinate [determinist](https://www.informationphilosopher.com/freedom/determinism.html) philosophers of science who hope to prove that [quantum indeterminacy](https://www.informationphilosopher.com/indeterminacy.html) does not exist. Einstein was correct that indeterminacy makes quantum theory a _discontinuous_ and _statistical_ theory. Its predictions and highly accurate experimental results are statistical in that they depend on an _ensemble_ of identical experiments, not on any individual experiment. Einstein wanted physics to be a _continuous_ field theory, in which all physical variables are completely and "locally" determined by the four-dimensional field of "space-time" in his theory of relativity. In his [autobiography](https://www.informationphilosopher.com/solutions/scientists/einstein/autobiography.html), fifteen years after EPR, Einstein explained his problem in very simple terms "Does a particle have a position in the moments just before it is measured?" If not, the quantum theory is _incomplete_. Since quantum theory says the particle may have a number of possible positions, with calculable probabilities, it is not only an incomplete theory, it is a theory with [alternative possibilities](https://www.informationphilosopher.com/freedom/possibilities.html). Einstein saw this as is in conflict with his idea of an external _objective_ reality independent of our _subjective_ experiments. In the "block universe" of Einstein's relativistic field theory, there is only one actual past, with determinate positions for a particle at all past times. Einstein's theory is [causal](https://www.informationphilosopher.com/freedom/causality.html). Quantum theory is [acausal](https://www.informationphilosopher.com/freedom/causa_sui.html). Better perhaps is to call it _statistically_ causal, since it also gives us a [statistical determinism](https://www.informationphilosopher.com/freedom/adequate_determinism.html), when we average over enough indeterministic microscopic events.. But Einstein was also bothered by what is now known as "nonlocality." Einstein mistakenly interpreted this [mysterious](https://www.informationphilosopher.com/freedom/mysteries.html) phenomenon seen in Bell's version of the EPR experiments as the _apparent_ transfer of something physical faster than the speed of light. ## The Collapse of the Two-Particle Wave Function What happens actually is a realization of one of two possible quantum states which quantum mechanics describes as in a [superposition](https://www.informationphilosopher.com/quantum/principles/#superposition). When this involves a single electron it demonstrates the fundamental [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html) of quantum mechanics. If ψ+ (spin-up) and ψ- (spin-down) are both solutions of the Schrödinger equation, then a linear combination of these, | ψ > = 1/√2 | ψ+ > + 1/√2 | ψ- >, with probability amplitude coefficients 1/√2, describes a solution in which the probability of either state is 1/2. When measured many times, such a superposed state will produce approximately 1/2 spin-up and 1/2 spin-down results. But when it involves two electrons widely separated in space, the indeterministic outcome of Schrödinger's two-particle wave function seems physically unacceptable to many. [Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) was the first person to see the "collapse" of a light wave as a quantum of light is absorbed in its entirety by a single electron. He also saw that the spherical wave seems to do something over large distances faster than the speed of light Einstein had first suspected "nonlocal" behavior in 1905 in his paper on the light-quantum hypothesis. How, he wondered, could a spherical wave of energy, spread out in a large volume of space, gather itself together instantly to be absorbed as a complete unit by a tiny atom? The heart of the problem of nonlocality is nothing more than the instantaneous ["collapse" of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). But in EPR we have a _two_-particle wave-function describing the "entangled" particles, instead of a one-particle wave function interfering with itself, as in the [two-slit experiment.](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/). The [1935 EPR paper](https://www.informationphilosopher.com/solutions/scientists/einstein/EPR.html) was based on an earlier question of Einstein's about two particles fired in opposite directions from a central source with equal velocities. He imagined them starting at _t0_ some distance apart and approaching one another with high velocities. Then for a short time interval from _t1_ to _t1 + Δt_ the particles are in contact with one another. Einstein described this situation to [Léon Rosenfeld](https://www.informationphilosopher.com/solutions/scientists/rosenfeld/) in 1933. Shortly before he left Germany to emigrate to America, Einstein attended a lecture on quantum electrodynamics by Rosenfeld. Keep in mind that Rosenfeld was perhaps the most dogged defender of the [Copenhagen Interpretation](https://www.informationphilosopher.com/quantum/copenhagen/), which maintains that a particle has no properties until it is measured. After the talk, Einstein asked Rosenfeld, “What do you think of this situation?” > Suppose two particles are set in motion towards each other with the same, very large, momentum, and they interact with each other for a very short time when they pass at known positions. Consider now an observer who gets hold of one of the particles, far away from the region of interaction, and measures its momentum: then, from the conditions of the experiment, he will obviously be able to deduce the momentum of the other particle. If, however, he chooses to measure the position of the first particle, he will be able tell where the other particle is. > > > (_Niels Bohr, His Life and Work as seen by His Friends and Colleagues_, 1967, S. Rozental, pp.128-129) Most misleading and confusing accounts of entanglement and nonlocality begin with the idea that _distinguishable_ particles _separate_ - particle 1 goes one way and particle 2 the other. After the particles interact at _t1_, quantum mechanics describes them with a single two-particle wave function that is not the product of independent particle wave functions. Because electrons, for example, are _indistinguishable_ particles, it is not proper to say electron 1 goes this way and electron 2 that way. (Nevertheless, it is convenient to label the particles - _after subsequent measurements_ - as we do in illustrations below.) Until the next measurement, it is misleading to think that specific particles have distinguishable paths. Einstein said correctly that at a later time _t2_, a measurement of one particle's position would instantly establish the position of the other particle - _without measuring it explicitly_. No interaction with the second particle is involved. Schrödinger described the two particles as "entangled" (_verschränkt_) at their first measurement, so EPR "nonlocal" phenomena are also known as "quantum entanglement." Note that Einstein _implicitly_ used _conservation of linear momentum_ to calculate the position of the second particle. Although conservation laws are rarely cited as the explanation, they are the physical reason that entangled particles _always_ produce perfectly correlated results. If the results were not always correlated, the implied violation of a fundamental conservation law would be a much bigger story than entanglement itself, as interesting as that is. We can diagram a simple case of Einstein’s question as follows, with indistinguishable electrons separating from their point of interaction to be measured at a later rime when they are far apart.  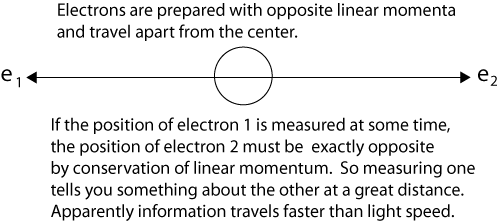This idea of something measured in one place "influencing" measurements far away challenged what Einstein thought of as "local reality." It came to be known as "[nonlocality](https://www.informationphilosopher.com/problems/nonlocality/)." In 1947, Einstein called it "_spukhaft Fernwirkung_" or "spooky action at a distance." From our standpoint of information philosophy, it is better to think of it as "knowledge-at-a-distance." Einstein had objected publicly to nonlocal phenomena as early as the Solvay Conference of 1927, when he criticized the [collapse of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) as "instantaneous-action-at-a-distance." He said that the probability wave could not act simultaneously at different places on the screen, which are in a "space-like" separation, without violating his theory of relativity. Einstein's criticism resembles the criticisms of Newton's theory of gravitation. Newton's opponents charged that his theory was "action at a distance" and instantaneous. Einstein's own theory of general relativity shows that gravitational "influences" travel at the speed of light and are mediated by a gravitational field that shows up as curved space-time. An allowable "action-at-a-distance" is one that is caused by "local" events, those in its past light-cone. Both gravitation and electromagnetism are _field_ theories, in which physical variables are functions of the four "local" space-time coordinates of Einstein's theory of relativity. Any disturbance at one point in the field can only "influence" another distant point by propagating to that point at the speed of light or less. But the quantum-mechanical wave-function is different. It is neither matter nor energy, nothing physical, only information and a "probability amplitude" whose square gives us probabilities and intensities of quantum phenomena. When a probability function collapses to unity in one place and zero elsewhere, nothing physical is moving from one place to the other. When the nose of one horse crosses the finish line, its probability of winning goes to certainty, and the finite probabilities of the other horses, including the one in the rear, instantaneously drop to zero. This happens faster than the speed of light, since the last horse is in a "space-like" separation. The first practical and workable experiments to test the EPR paradox were suggested by [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/) (though they were not realized for almost two decades). Instead of only linear momentum, Bohm proposed using two electrons that are prepared in an initial state of known total spin. If one electron spin is 1/2 in the up direction and the other is spin down or -1/2, the total spin is zero. The underlying physical law of importance is another momentum conservation law, in this case the conservation of total spin angular momentum. If electron 1 is prepared with spin down and electron 2 with spin up, the total angular momentum or spin is zero. This is called the singlet state.  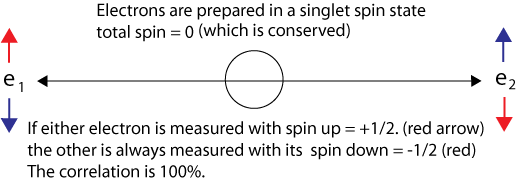Quantum theory describes the two electrons as in a superposition of states, the first state spin up ( + ) and spin down ( - ), the second state spin down ( - ) and spin up ( + ), | _ψ_ > = (1/√2) | _+_ _-_ > - (1/√2) | _-_ _+_ > The standard theory of quantum mechanics says that the prepared system is in a linear combination (or superposition) of these two states, and can provide only the probabilities of finding the entangled system in either the | _+_ _-_ > state or the | _-_ _+_ > state. Quantum mechanics does not describe the paths or the spins of the individual particles. Note that should measurements result in | _+_ _+_ > or | _-_ _-_ > state, that would violate the conservation of angular momentum. We call the conserved total spin a ["hidden constant of the motion"](https://www.informationphilosopher.com/quantum/hidden_constant/). In 1964, [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) showed how the 1935 "thought experiments" of Einstein, Podolsky, and Rosen (EPR) could be made into real physical experiments, following the ideas of David Bohm. Bell developed a theorem that puts limits on Bohm's "hidden variables" that might restore a deterministic physics. Bell's theorem takes the form of what he called an inequality, the violation of which would confirm standard quantum mechanics. Since Bell's work, many other physicists have defined other "Bell inequalities" and developed increasingly sophisticated experiments to test them. EPR tests can be done more easily with polarized photons than with electrons, which require complex magnetic fields. The first of these was done in 1972 by Stuart Freedman and [John Clauser](http://en.wikipedia.org/wiki/John_Clauser) at UC Berkeley. They used oppositely polarized photons (one with spin = +1, the other spin = -1) coming from the central source. Again, the total photon spin of zero is conserved (our ["hidden constant"](https://www.informationphilosopher.com/quantum/hidden_constant/)). Their data, in agreement with quantum mechanics, violated the Bell's inequalities to high statistical accuracy, thus providing strong evidence against _local_ hidden-variable theories. For more on the principle of _superposition of states_ and the physics of photons, see the [Dirac 3-polarizers experiment](https://www.informationphilosopher.com/solutions/experiments/dirac_3-polarizers/). [John Clauser, Michael Horne, Abner Shimony, and Richard Holt](http://en.wikipedia.org/wiki/CHSH_inequality) (known collectively as CHSH) and later [Alain Aspect](http://en.wikipedia.org/wiki/Alain_Aspect) did even more sophisticated tests. The outputs of the polarization analyzers were fed to a coincidence detector that records the instantaneous measurements, described as + -, - +, + +, and - - . The first two ( + - and - + ) conserve the spin angular momentum and are the only types ever observed in these nonlocality/entanglement tests (provided both experiments measure at the same angle).  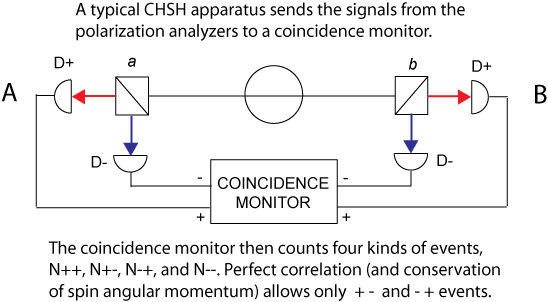With the exception of some of Holt's early results that were found to be erroneous, _no evidence has so far been found of any failure of standard quantum mechanics_. And as experimental accuracy has improved by orders of magnitude, quantum physics has correspondingly been confirmed to one part in 1014, and the speed of the probability of any "information transfer" between particles has a lower limit of 106 times the speed of light. There has been no evidence for _local_ "hidden variables." Nevertheless, wishful-thinking experimenters continue to look for possible "loopholes" in the experimental results, such as detector inefficiencies that might be hiding results favorable to Einstein's picture of "local reality." ## How Information Physics Helps To "Explain" EPR Nonlocality Information physics starts with the fact that measurements bring new stable [information](https://www.informationphilosopher.com/introduction/information/) into existence. In EPR the information in the prepared state of the two particles includes the fact that the total linear momentum and the total angular momentum are zero. New information requires an irreversible process that also increases the entropy more than enough to compensate for the information increase, to satisfy the second law of thermodynamics. It is this moment of irreversibility and the creation of new _observable_ information that is the "cut" or Schnitt" described by [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/) and [John von Neumann](https://www.informationphilosopher.com/solutions/scientists/neumann/) in the famous [problem of measurement](https://www.informationphilosopher.com/problems/measurement/) Note that the new observable information does not require a "[conscious observer](https://www.informationphilosopher.com/problems/measurement/#conscious_observer)" as [Eugene Wigner](https://www.informationphilosopher.com/solutions/scientists/wigner/) and some other scientists thought. The information is _ontological_ (really in the world) and not merely _epistemic_ (in the mind). Without new information, there would be nothing for the observers to observe. ### Initially Prepared Information Plus Conservation Laws Conservation laws are the consequence of extremely deep properties of nature that arise from simple considerations of symmetry. We regard these laws as "cosmological principles." Physical laws do not depend on the absolute place and time of experiments, nor their particular direction in space. Conservation of linear momentum depends on the translation invariance of physical systems, conservation of energy the independence of time, and conservation of angular momentum the invariance under rotations. Recall that the EPR experiment starts with two electrons (or photons) prepared in an entangled state that is a linear combination of pure two-particle states, each of which conserves the total angular momentum and, of course, conserves the linear momentum as in Einstein's original EPR example. This information about the linear and angular momenta is established by the initial state preparation (a measurement). Quantum mechanics describes the probability amplitude wave function _ψ_ of the two-particle system as in a _superposition_ of two-particle states. It is _not separable_ into a product of single-particle states, and there is no information about the identical _indistinguishable_ electrons traveling along _distinguishable_ paths. | _ψ_ > = (1/√2) | _+_ _-_ > - (1/√2) | _-_ _+_ >         (1) The probability amplitude wave function _ψ_ travels from the source (at the speed of light or less). Let's assume that at _t1_ observer A finds an electron (e1) with spin up. After the "first" measurement, new information comes into existence telling us that the wave function _ψ_ has "collapsed" into the state | _+_ _-_ >. Just as in the [two-slit experiment](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/), probabilities have now become certainties. If the "first" measurement finds electron 1 is spin up, so the entangled electron 2 must be found in a "second" measurement with spin down to conserve angular momentum. And conservation of linear momentum tells us that at _t1_ the second electron is equidistant from the source in the opposite direction. As with any [wave-function collapse](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/), the probability amplitude information "travels" instantly. But unlike the [two-slit experiment](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/), where the collapse goes to a specific point in 3-dimensional configuration space, the "collapse" here is a "jump" or "projection" into one of the two possible 6-dimensional two-particle quantum states | _+_ _-_ > or | _-_ _+_ >. This makes "visualization" (Schrödinger's _Anschaulichkeit_) more difficult, but the parallel with the collapse in the two-slit case provides an intuitive insight of sorts. If the "first" measurement finds an electron (call it electron 1) as spin-up, then at that moment of new information creation, the two-particle wave function collapses to the state | _+_ _-_ > and electron 2 "jumps" into a spin-down state with probability unity (certainty). The results of observer B's "second" measurement (usually assumed to be at a later time _t2_, but _t1_ at the earliest, or it would be the "first" measurement) is therefore _determined_ to be spin down. Notice that [Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/)'s intuition that the result seems already "determined" or "fixed" before the second measurement is in part correct. The result is determined by the law of conservation of momentum (within the usual uncertainty) and the spin is completely determined. But as with the distinction between [determinism](https://www.informationphilosopher.com/freedom/determinism.html) and [_pre_-determinism](https://www.informationphilosopher.com/freedom/pre-determinism.html) in the [free-will](https://www.informationphilosopher.com/freedom/free-will.html) debates, the measurement by observer B was not pre-determined _before_ observer A's measurement. It was simply _determined by_ her measurement. ### Why do so few accounts of EPR mention conservation laws? Although Einstein mentioned conservation in the original EPR paper, it is noticeably absent from later work. A prominent exception is [Eugene Wigner](https://www.informationphilosopher.com/solutions/scientists/wigner/), writing on the [problem of measurement](https://www.informationphilosopher.com/problems/measurement/) in 1963: > If a measurement of the momentum of one of the particles is carried out — the possibility of this is never questioned — and gives the result **p**, the state vector of the other particle suddenly becomes a (slightly damped) plane wave with the momentum -**p**. This statement is synonymous with the statement that a measurement of the momentum of the second particle would give the result -**p**, as follows from the conservation law for linear momentum. The same conclusion can be arrived at also by a formal calculation of the possible results of a joint measurement of the momenta of the two particles. > > One can go even further: instead of measuring the linear momentum of one particle, one can measure its angular momentum about a fixed axis. If this measurement yields the value _mℏ_, the state vector of the other particle suddenly becomes a cylindrical wave for which the same component of the angular momentum is -_mℏ_. This statement is again synonymous with the statement that a measurement of the said component of the angular momentum of the second particle certainly would give the value -_mℏ_. This can be inferred again from the conservation law of the angular momentum (which is zero for the two particles together) or by means of a formal analysis. Hence, a "contraction of the wave packet" took place again. > > It is also clear that it would be wrong, in the preceding example, to say that even before any measurement, the state was a mixture of plane waves of the two particles, traveling in opposite directions. For no such pair of plane waves would one expect the angular momenta to show the correlation just described. This is natural since plane waves are not cylindrical waves, or since [the state vector has] properties different from those of any mixture. The statistical correlations which are clearly postulated by quantum mechanics (and which can be shown also experimentally, for instance in the Bothe-Geiger experiment) demand in certain cases a "reduction of the state vector." The only possible question which can yet be asked is whether such a reduction must be postulated also when a measurement with a macroscopic apparatus is carried out. [Considerations] show that even this is true if the validity of quantum mechanics is admitted for all systems. > > (_The Problem of Measurement_, Eugene Wigner, in Wheeler and Zurek, p,340) ## Visualizing Entanglement and Nonlocality [Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/) said that his "Wave Mechanics" provided more "visualizability" (_Anschaulichkeit_) than the "damned quantum jumps" of the Copenhagen school, as he called them. He was right. But we must focus on the probability amplitude wave function of the prepared two-particle state, and not attempt to describe the paths or locations of independent particles - at least until _after_ some measurement has been made. We must also keep in mind the conservation laws that Einstein used to describe nonlocal behavior in the first place. Then we can see that the "[mystery](https://www.informationphilosopher.com/freedom/mysteries.html)" of _nonlocality_ for two particles is primarily the same mystery as the single-particle [collapse of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). But there is an extra mystery, one we might call an "enigma," of the _nonseparability_ of identical indistinguishable particles. As [Richard Feynman](https://www.informationphilosopher.com/solutions/scientists/feynman/#mystery) said, there is _only one mystery_ in quantum mechanics (the superposition of states, the probabilities of collapse into one state, and the consequent statistical outcomes). The only difference in two-particle entanglement and nonlocality is that two particles appear simultaneously (in their original interaction frame) when their wave function collapses. > We choose to examine a phenomenon which is impossible, _absolutely_ impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the _only_ mystery. We cannot make the mystery go away by "explaining" how it works. We will just _tell_ you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics. > > (_The Feynman Lectures on Physics_, vol III, 1-1) In his 1935 paper (and his correspondence with Einstein), Schrödinger described the two particles in EPR as "entangled" in English, _verschränkt_ in German, which means something like cross-linked. It describes someone standing with arms crossed. In the time evolution of an entangled two-particle state according to the Schrödinger equation, we can visualize it - as we visualize the single-particle wave function - as collapsing when a measurement is made. The discontinuous “jump” is also described as the “reduction of the wave packet.” This is apt in the two-particle case, where the superposition of _| + - >_ and _| - + >_ states is “projected” or “reduced" to one of these states, say _| - + >_, and then further "reduced" to the product of independent one-particle states, _| - >| + >_. Measurement of a two-particle wave function measures both particles, reducing them to _separate_ one-particle wave functions, after which they are no longer entangled. When entangled, the particles are _nonseparable_. Once measured, they are separate quantum systems with their own wave functions _| - >and | + >_. They are no longer entangled. In the two-particle case (instead of just one particle making an appearance), when either particle is measured we know instantly the now determinate properties of the other particle. They are the properties that satisfy the conservation laws, including its location equidistant from, but on the opposite side of the source, with the complementary (opposite) spin. In the one-particle case, it has no definite position before the experiment, then it appears somewhere. For two particles, neither one has a position, then both appear simultaneously (in an appropriate frame of reference), with total momenta, positions, and spins conserved. . ## Animation of a two-particle wave function collapsing - [click to restart](https://www.informationphilosopher.com/solutions/experiments/EPR/)  Compare the collapse of the two-particle probability amplitude above to the [single-particle collapse here](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). Some commentators say that nonlocality and entanglement are a "second revolution" in quantum mechanics, "the greatest mystery in physics," or "science's strangest phenomenon," and that quantum physics has been "reborn." They usually quote Erwin Schrödinger as saying > "I consider [entanglement] not as one, but as _the_ characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought." Schrödinger knew that his two-particle wave function could not have the same simple interpretation as the single particle, which can be visualized in ordinary 3-dimensional configuration space. And he is right that entanglement exhibits a richer form of the "action-at-a-distance" and nonlocality that Einstein had already identified in the [collapse of the single particle wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). But the main difference is that _two_ particles acquire new properties instead of one, and they do it instantaneously (at faster than light speeds), just as in the case of a single-particle measurement, where the finite probability of appearing at various distant locations collapses to zero at the instant the particle is found somewhere. ## Can a Special Frame Help Resolve the EPR Paradox? Almost every presentation of the EPR paradox begins with something like "Alice observes one particle..." and concludes with the question "How does the second particle get the information needed so that Bob's measurements correlate perfectly with Alice?" There is a fundamental asymmetry in this framing of the EPR experiment. It is a surprise that Einstein, who was so good at seeing deep symmetries, did not consider how to remove the asymmetry. Consider this reframing: Alice's measurement collapses the two-particle wave function. The two indistinguishable particles simultaneously appear at locations in a space-like separation. The frame of reference in which the source of the two entangled particles and the two experimenters are at rest is a special frame in the following sense. As Einstein knew very well, there are frames of reference moving with respect to the laboratory frame of the two observers in which the time order of the events can be reversed. In some moving frames Alice measures first, but in others Bob measures first. If there is a special frame of reference (not a preferred frame in the relativistic sense), surely it is the one in which the origin of the two entangled particles is at rest. Assuming that Alice and Bob are also at rest in this special frame and equidistant from the origin, we arrive at the simple picture in which any measurement that causes the two-particle wave function to collapse makes both particles appear simultaneously at determinate places with fully correlated properties (just those that are needed to conserve energy, momentum, angular momentum, and spin).  In the two-particle case (instead of just one particle making an appearance), when either particle is measured, we know instantly those properties of the other particle that satisfy the conservation laws, including its location equidistant from, but on the opposite side of, the source, and its other properties such as spin. We can also ask what happens if Bob is not at the same distance from the origin as Alice. This introduces a positional asymmetry. But there is still no time asymmetry from the point of view of the two-particle wave function collapse. When Alice detects the particle (with say spin up), at that instant the other particle also becomes determinate (with spin down) at the same distance on the other side of the origin. It now continues, in that determinate state, to Bob's measuring apparatus.  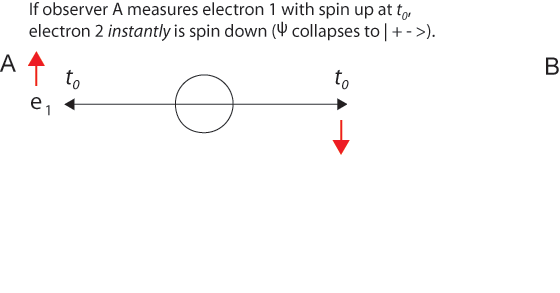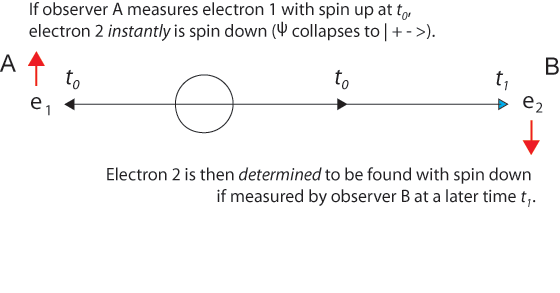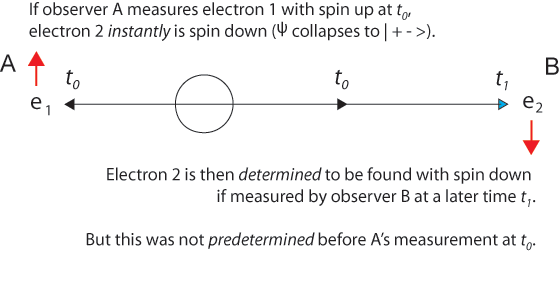Einstein asked whether the particle has a determinate position (or spin) just before it is measured. Even if it does not, we can say that the electron spin was determined from the moment the two-particle wave function collapsed. Recall that the two-particle wave function describing the indistinguishable particles cannot be separated into a product of two single-particle wave functions. When either particle is measured, they both become determinate. --- ## Influences from Outside Space and Time, Even Back from the Future! **Superdeterminism** During a mid-1980's interview by BBC Radio 3 organized by P. C. W. Davies and J. R. Brown, Bell proposed the idea of a "_[superdeterminism](https://www.informationphilosopher.com/solutions/experiments/EPR/freedom/superdeterminism.html)_" that could explain the correlation of results in two-particle experiments without the need for faster-than-light signaling. The two experiments need only have been [_pre_-determined](https://www.informationphilosopher.com/freedom/pre-determinism.html) by causes reaching both experiments from an earlier time. > _I was going to ask whether it is still possible to maintain, in the light of experimental experience, the idea of a [deterministic](https://www.informationphilosopher.com/solutions/experiments/EPR/freedom/determinism.html) universe?_ > > You know, one of the ways of understanding this business is to say that the world is super-deterministic. That not only is inanimate nature deterministic, but we, the experimenters who imagine we can choose to do one experiment rather than another, are also determined. If so, the difficulty which this experimental result creates disappears. > > _Free will is an [illusion](https://www.informationphilosopher.com/solutions/experiments/EPR/freedom/illusionism.html) - that gets us out of the crisis, does it?_ > > That's correct. In the analysis it is assumed that free will is genuine, and as a result of that one finds that the intervention of the experimenter at one point has to have consequences at a remote point, in a way that influences restricted by the finite velocity of light would not permit. If the experimenter is not free to make this intervention, if that also is determined in advance, the difficulty disappears. > > > (_The Ghost in the Atom_, P.C.W. Davies and J. Brown, ch.3, p.47) Bell's superdeterminism would deny the important "[free choice](https://www.informationphilosopher.com/freedom/free_choice.html)" of the experimenter (originally suggested by [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/) and [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/)) and later explored by [John Conway](https://www.informationphilosopher.com/solutions/scientists/conway/) and [Simon Kochen](https://www.informationphilosopher.com/solutions/scientists/kochen/). Conway and Kochen claim that the experimenters' free choice requires that atoms must have [free will](https://www.informationphilosopher.com/freedom/free_will.html), something they call their [Free Will Theorem](https://www.informationphilosopher.com/freedom/free_will_theorem.html). In his 1996 book, _Time's Arrow and Archimedes' Point_, Price proposes an Archimedean point "outside space and time" as a solution to the problem of nonlocality in the Bell experiments in the form of an "advanced action." Rather than a "[superdeterministic](https://www.informationphilosopher.com/freedom/superdeterminism.html)" common cause coming from "outside space and time" (as proposed by Bell, Gisin, Suarez, and others), Price argues that there might be a cause coming backwards in time from some interaction in the future. [Roger Penrose](https://www.informationphilosopher.com/solutions/scientists/penrose/) and [Stuart Hameroff](https://www.informationphilosopher.com/solutions/scientists/hameroff/#backward) have also promoted this idea of "backward causation," sending information backward in time in the [Libet experiments](https://www.informationphilosopher.com/freedom/libet_experiments.html) and in the [EPR experiments](https://www.informationphilosopher.com/solutions/experiments/EPR/). John Cramer's [Transactional Interpretation](http://en.wikipedia.org/wiki/Transactional_interpretation) of quantum mechanics and other [Time-Symmetric Interpretations](http://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics#Time-symmetric_theories) like that of Yakir Aharonov and K. B Wharton also search for Archimedean points "ouside space and time." [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/#BBC), and more recently, following Bell, [Nicholas Gisin](https://www.informationphilosopher.com/solutions/scientists/gisin/) and [Antoine Suarez](https://www.informationphilosopher.com/solutions/scientists/suarez/) claim that something might be coming from "outside space and time" to correlate the results in the spacelike-separated experimental tests of [Bell's Theorem](https://www.informationphilosopher.com/solutions/experiments/bells_theorem/). Gisin and his colleagues have extended the polarized photon tests of EPR and the [Bell inequalities](https://www.informationphilosopher.com/solutions/experiments/bells_theorem/) to a separation of 18 kilometers near Geneva. They continue to find 100% correlation and no evidence of the "hidden variables" sought after by Einstein and [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/). An interesting use of the special theory of relativity was proposed by Gisin's colleagues, [Antoine Suarez](https://www.informationphilosopher.com/solutions/scientists/suarez/) and Valerio Scarani. Their "Before-Before" experiment uses the idea of hyperplanes of simultaneity. Back in the 1960's, [C. W. Rietdijk](https://www.informationphilosopher.com/solutions/philosophers/rietdijk/) and [Hilary Putnam](https://www.informationphilosopher.com/solutions/philosophers/putnam/) argued that physical [determinism](https://www.informationphilosopher.com/freedom/determinism.html) could be proved to be true by considering the experiments and observers A and B in the above diagram to be moving at high speed with respect to one another. [Roger Penrose](https://www.informationphilosopher.com/solutions/scientists/penrose/) developed a similar argument in his book _The Emperor's New Mind_. It is called the [Andromeda Paradox](https://www.informationphilosopher.com/solutions/scientists/penrose/#Andromeda_Paradox). Suarez and Scarani showed that for some relative speeds between the two observers A and B, observer A could "see" the measurement of observer B to be in his future, and vice versa. This is why we need the special frame above to understand entanglement. Because the two experiments have a "space-like" separation (neither is inside the causal light cone of the other), each observer thinks he does his own measurement before the other. Gisin tested the limits on this effect by moving mirrors in the path to the birefringent crystals and showed that, like all other Bell experiments, the "_Before-Before_" suggestion of Suarez and Scarani did nothing to invalidate quantum mechanics. These experiments were able to put a lower limit on the speed with which the information about probabilities collapses, estimating it as at least thousands - perhaps millions - of times the speed of light and showed empirically that probability collapses are essentially instantaneous. Despite all his experimental tests verifying quantum physics, including the "reality" of nonlocality and entanglement, Gisin continues to explore the EPR paradox, considering the possibility that signals are coming to the entangled particles from "outside space-time." ## EPR "Loopholes" and Free Will Investigators who try to recover the "elements of local reality" that Einstein wanted, and who hope to eliminate the irreducible randomness of quantum mechanics that follows from wave functions as probability amplitudes, often cite "loopholes" in EPR experiments. For example, the "detection loophole" claims that the efficiency of detectors is so low that they are missing many events that might prove Einstein was right. Most all the loopholes have now been closed, but there is one loophole that can never be closed because of its metaphysical/philosophical nature. That is the "[(pre-)determinism](https://www.informationphilosopher.com/freedom/pre-determinism.html) loophole." If every event occurs for reasons that were established at the beginning of the universe, then all the careful experimental results are meaningless. [John Conway](https://www.informationphilosopher.com/solutions/scientists/conway/) and [Simon Kochen](https://www.informationphilosopher.com/solutions/scientists/kochen/) have formalized this loophole in what they call the [Free Will Theorem](https://www.informationphilosopher.com/freedom/free_will_theorem.html). Although Conway and Kochen do not claim to have proven free will in humans, they assert that should such a freedom exist, then the same freedom must apply to the elementary particles. What Conway and Kochen are really describing is the [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html) that quantum mechanics has introduced into the world. Although indeterminism is a [requirement](https://www.informationphilosopher.com/freedom/requirements.html) for human freedom, it is insufficient by itself to provide both ["free" _and_ "will"](https://www.informationphilosopher.com/freedom/free_will.html). Indeterminism works primarily to block [_pre_-determinism](https://www.informationphilosopher.com/freedom/pre-determinism.html). Without indeterminism, _no new information could be created_ in the universe.