# Interpretations of Quantum Mechanics Wikipedia has a most comprehensive page on the [Interpretations of Quantum Mechanics](https://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics). As with our analysis of [positions on the free will problem](https://www.informationphilosopher.com/freedom/taxonomy.html), there are many interpretations, some very popular (with many adherents), some with only a few supporters. The popular views are defended in hundreds or journal articles and published books. Just as with philosophers, the supporters of an interpretation often have their own jargon which sometimes makes communication between the different positions difficult. The standard "orthodox" interpretation of quantum mechanics includes a _projection postulate_. This is the idea that once one of the [_possible_](https://www.informationphilosopher.com/freedom/possibilities.html) locations for a particle becomes [_actual_](https://www.informationphilosopher.com/freedom/actualism.html) at one position, the probabilities for actualization at all other positions becomes instantly zero. This sudden disappearance of possibilities/probabilities at locations remote from where a particle is actually found is called [nonlocality](https://www.informationphilosopher.com/problems/nonlocality/). It was first seen as early as 1905 by [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/). "Projection" or "reduction of the wave packet" is known as the "[collapse of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/)," although the wave itself function does not "collapse" in the sense of gathering itself together at the single point where a particle is found. All that changes is our [knowledge](https://www.informationphilosopher.com/knowledge/) about the particle, where it is actually found. What changes is only _abstract immaterial_ [information](https://www.informationphilosopher.com/introduction/information/) about the particle's location. In the [two-slit experiment](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/), for example, the wave function actually does not change at all, since it just depends on the boundary conditions in the experiment, which do not change because one particle has been found. Every future experiment with the same conditions has exactly the same wave function and thus the same probabilities for finding a particle. Unless, of course, we change from one slit open to both open, or vice versa. Another similar particle entering the same space, after the first particle has been detected and thus removed from the space, would have the same probability distribution, since the wave function is determined by the solution of the Schrödinger equation, given the boundary conditions for the space and the wavelength of the particle. The wave function is simply _immaterial_ information. It remains a mystery how it controls (if it controls) the motions of individual particles so their the predicted probabilities agree perfectly with the statistics of large numbers of identical experiments. Today there appear to be about as many unorthodox interpretations, denying [Paul Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/) projection postulate, as there are more standard views. ## No-Collapse Interpretations [Pilot-Wave Theory](http://en.wikipedia.org/wiki/De_Broglie%E2%80%93Bohm_theory) - deterministic, non-local, hidden variables, no observer, particles (de Broglie-Bohm, 1952) [Many-Worlds Interpretation](http://en.wikipedia.org/wiki/Many-worlds_interpretation) - deterministic, local, hidden variables, no observer (Everett-De Witt, 1957) [Time-Symmetric Theory](http://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics#Time-symmetric_theories) (Aharonov, 1964) [Decoherence](http://en.wikipedia.org/wiki/Decoherence) - deterministic, local, no particles (Zeh-Zurek, 1970) [Consistent Histories](http://en.wikipedia.org/wiki/Consistent_histories) - local (Griffiths-Omnès-Gell-Mann-Hartle, 1984) [Consistent Histories](http://en.wikipedia.org/wiki/Consistent_histories) - local (Griffiths-Omnès-Gell-Mann-Hartle, 1984) [Cosmological Interpretation](https://www.informationphilosopher.com/introduction/physics/interpretations/arxiv.1008.1066.pdf) (Aguirre and Tegmark, 2012) Collapse Interpretations [Copenhagen Interpretation](https://www.informationphilosopher.com/introduction/physics/Copenhagen_Interpretation.html) - indeterministic, non-local, observer (Bohr-Heisenberg-Born-Jordan, 1927) [Conscious Observer](http://en.wikipedia.org/wiki/Interpretation_of_quantum_mechanics#von_Neumann.2FWigner_interpretation:_consciousness_causes_the_collapse) - indeterministic, non-local, observer (Von Neumann-Wigner) [Statistical Ensemble](http://en.wikipedia.org/wiki/Ensemble_Interpretation) - indeterministic, non-local, no observer (Einstein-Born- Ballentine) [Objective Collapse](http://en.wikipedia.org/wiki/Objective_collapse_theory) - indeterministic, non-local, no observer (Ghirardi-Rimini-Weber, 1986; Penrose, 1989) [Transactional Interpretation](http://en.wikipedia.org/wiki/Transactional_interpretation) - indeterministic, non-local, no observer, no particles (Cramer, 1986) [Relational Interpretation](http://en.wikipedia.org/wiki/Relational_quantum_mechanics) - local, observer (Rovelli, 1994) [Pondicherry Interpretation](http://arxiv.org/pdf/quant-ph/0412182.pdf) - indeterministic, non-local, no observer (Mohrhoff, 2005) [Information Interpretation](https://www.informationphilosopher.com/introduction/physics/interpretation) - indeterministic, non-local, no observer (Doyle, 2015) From the earliest days of quantum theory, when [Max Planck](https://www.informationphilosopher.com/solutions/scientists/planck/) in 1900 hypothesized an abstract "quantum of action" and [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) in 1905 hypothesized that energy comes in physical quanta, there have been disagreements about "interpretations," misunderstandings about the underlying "reality" of the external world that could account for the apparent agreement between quantum theory and the observed experimental facts. For example, the inventor of the quantum of action used his constant _h_ as a heuristic device to calculate the probabilities of various virtual oscillators (distributing them among energy states using Boltzmann's statistical mechanics ideas, the partition function, etc.). He quantized these mechanical oscillators, but not the radiation field itself. In 1913, Bohr similarly quantized the oscillators (electrons) in the "old quantum theory" and his planetary model of the electrons orbiting the Rutherford nucleus. Bohr's electrons "jump" discontinuously from orbit to orbit, emitting or absorbing discrete amounts of energy _En - Em_ where _n_ and _m_ are orbital "quantum numbers." But Bohr insisted that the energy radiated in a quantum jump was continuous, ignoring Einstein's hypothesis. In 1905, Einstein wrote, "the energy of a light ray spreading out from a point source is not continuously distributed over an increasing space but consists of a finite number of energy quanta which are localized at points in space, which move without dividing, and which can only be produced and absorbed as whole units." By comparison to Planck, Einstein had already in 1905 quantized the continuous electromagnetic radiation field as light quanta (today's photons). Planck denied the physical "reality" of any quanta (including his own) until 1910 at the earliest. And Bohr did not accept photons as being emitted and absorbed during quantum jumps until twenty years after Einstein proposed them - if then. Photons are now universally accepted, of course, and (sadly) standard quantum mechanics says they are emitted and absorbed during Bohr's "quantum jumps" of the electrons. Einstein saw clearly that if the radiation emitted by an atom were to spread out diffusely as a classical wave into a large volume of space, how could the energy collect itself together again instantly to be absorbed by another atom - without having that energy travel faster than light speed as it gathered itself together in the absorbing atom? He clearly saw that a discrete, discontinuous "jump" was involved, something denied by many of the modern "interpretations" of quantum mechanics. He also saw that the wave that filled space moments before the detection of the whole quantum of energy must disappear instantly as all the energy in the quantum is absorbed by a single atom in a particular location. This was a collapse of a light wave twenty years before there was a "wave function" and [Erwin Schrōdinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/)'s wave equation! Later Einstein interpreted the wave at a point as the probability of light quanta at that point. many years before [Max Born](https://www.informationphilosopher.com/solutions/scientists/born/)'s statistical interpretation of the wave function! The idea of something (later called the wave function) associated with the particle led to the problem of [wave-particle duality](https://www.informationphilosopher.com/introduction/physics/wave-particle_duality.html), described first by Einstein in 1909. In 1927, he expressed concern that what came to be called [nonlocality](https://www.informationphilosopher.com/introduction/physics/interpretations/problems/nonlocality/) violates his special theory of relativity. To this day, it drives the idea that quantum physics cannot be reconciled with relativity. It can. The nadir of interpretation was probably the most famous interpretation of all, the one developed in Copenhagen, the one [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/)'s assistant Leon Rosenfeld said was not an interpretation at all, but simply the "standard orthodox theory" of quantum mechanics. It was the nadir of interpretation because Copenhagen wanted to put a stop to "interpretation" in the sense of understanding or "visualizing" an underlying reality. The Copenhageners said we should not try to "visualize" what is going on behind the collection of observable experimental data. Just as Kant said we could never know anything about the "thing in itself," the _Ding-an-sich_, so the positivist philosophy of Comte, Mach, Russell, and Carnap and the British empiricists Locke and Hume claim that [knowledge](https://www.informationphilosopher.com/knowledge/) stops at the "_secondary_" sense data or perceptions of phenomena, preventing access to the _primary_ "objects." Einstein's views on quantum mechanics have been seriously distorted (and his early work largely forgotten), perhaps because of his famous criticisms of [Born](https://www.informationphilosopher.com/solutions/scientists/born/)'s "statistical interpretation" and [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/)'s claim that quantum mechanics was "complete" without describing what particles are doing from moment to moment. Though its foremost critic, Einstein frequently said that quantum mechanics was a most successful theory, the very best theory so far at explaining microscopic phenomena, but that he hoped his ideas for a continuous field theory would someday add to the discrete particle theory and its "non-local" phenomena. It would allow us to get a deeper understanding of underlying reality, though at the end he despaired for his continuous field theory compared to particle theories. Many of the "interpretations" of quantum mechanics deny a central element of quantum theory, one that Einstein himself established in 1916, namely the role of [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html), or "[chance](https://www.informationphilosopher.com/freedom/chance.html)," to use its traditional name, as Einstein did in physics (in German, _Zufall_) and as [William James](https://www.informationphilosopher.com/solutions/philosophers/james/) did in philosophy in the 1880's. These interpretations hope to restore the [determinism](https://www.informationphilosopher.com/freedom/determinism.html) of classical mechanics. Einstein hoped for a return to deterministic physics, but even more important for him was a physics based on continuous fields, rather than discrete discontinuous particles. We can therefore classify various interpretations by whether they accept or deny chance, especially in the form of the so-called ["collapse" of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/), also known as the "reduction" of the wave packet or what [Paul Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/) called the "[projection postulate](https://www.informationphilosopher.com/introduction/physics/interpretations/#postulate)." Most "no-collapse" theories are deterministic. "Collapses" in standard quantum mechanics are irreducibly [indeterministic](https://www.informationphilosopher.com/freedom/indeterminism.html). And a great surprise is that the wave function in fact does not collapse! Many interpretations are attempts to wrestle with still another problem that Einstein saw as early as 1905, in "non-local" events something appears to be moving faster than light and thus violating his special theory of relativity (which he formulated in 1905). So we can classify interpretations by whether they accept the instantaneous nature of the collapse, especially the collapse of the two-particle wave function of "entangled" systems, where two particles appear instantly in widely separated places, with correlated properties that conserve energy, momentum, angular momentum, spin, etc. These interpretations are concerned about _nonlocality_ - the idea that "reality" is "nonlocal" with simultaneous events in widely separated places correlated perfectly - a sort of "action-at-a-distance." Many interpretations prefer wave mechanics to quantum mechanics, seeing wave theories as continuous field theories. They like to regard the wave function as a real entity rather than an abstract _possibilities function_. De Broglie's pilot-wave theory and its variations (e.g., Bohmian mechanics, Schrödinger's view) hoped to represent the particle as a "wave packet" composed of many waves of different frequencies, such that the packet has non-zero values in a small volume of space. Schrödinger and others found such a wave packet rapidly disperses . Finally, we may also classify interpretations by their definitions of what constitutes a "measurement," and particularly what they see as the famous ["problem of measurement](https://www.informationphilosopher.com/problems/measurement/)." Niels Bohr, Werner Heisenberg, and [John von Neumann](https://www.informationphilosopher.com/solutions/scientists/neuman/) had a special role for the "conscious observer"in a measurement. [Eugene Wigner](https://www.informationphilosopher.com/solutions/scientists/wigner/) claimed that the observer's conscious mind _caused_ the wave function to collapse in a measurement. So we have three major characterizations - indeterministic-discrete-discontinuous "collapse" vs. deterministic-continuous "no-collapse" theories, nonlocality-faster-than-light vs. local "elements of reality" in "realistic theories, and the role of the observer. Another way to look at an interpretation is to ask which basic element (or elements) of standard quantum mechanics does the interpretation question or just deny? For example, some interpretations deny the existence of particles. They admit only waves that evolve unitarily under the Schrōdinger equation. We can begin by describing those elements, using the formulation of quantum mechanics that Einstein thought most perfect, that of P. A. M. Dirac. --- ## A Brief Introduction to Basic Quantum Mechanics Einstein said of Dirac in 1930, "Dirac, to whom, in my opinion, we owe the most perfect exposition, logically, of this [quantum] theory" All of quantum mechanics rests on the Schrōdinger equation of motion that [deterministically](https://www.informationphilosopher.com/freedom/determinism.html) describes the time evolution of the [probabilistic](https://www.informationphilosopher.com/freedom/probability.html) wave function, plus three basic assumptions, the _principle of superposition_ (of wave functions), the _axiom of measurement_ (of expectation values for observables), and the _projection postulate_ (which describes the [collapse of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) that introduces [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html) or [chance](https://www.informationphilosopher.com/freedom/chance.html) during interactions). Dirac's "transformation theory" then allows us to "represent" the initial wave function (before an interaction) in terms of a "basis set" of "eigenfunctions" appropriate for the _possible_ quantum states of our measuring instruments that will describe the interaction. Elements in the "transformation matrix" immediately give us the _probabilities_ of measuring the system and finding it in one of the _possible_ quantum states or "eigenstates," each eigenstate corresponding to an "eigenvalue" for a dynamical operator like the energy, momentum, angular momentum, spin, polarization, etc. Diagonal (_n, n_) elements in the transformation matrix give us the eigenvalues for observables _in_ quantum state _n_. Off-diagonal (_n, m_) matrix elements give us transition probabilities _between_ quantum states _n_ and _m_. Notice the sequence - _possibilities > probabilities > actuality_: the wave function gives us the _possibilities_, for which we can calculate _probabilities_. Each experiment gives us one _actuality_. A very large number of identical experiments confirms our probabilistic predictions to thirteen significant figures (decimal places), the most accurate physical theory ever discovered. 1. _The Schrōdinger Equation_. The fundamental equation of motion in quantum mechanics is [Erwin Schrōdinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/)'s famous wave equation that describes the evolution in time of his wave function _ψ_. _iℏ δψ / δt = H ψ_         (1) Max Born interpreted the square of the absolute value of Schrōdinger's wave function |_ψn |2_ (or < _ψn | ψn_ > in Dirac notation) as providing the [probability](https://www.informationphilosopher.com/freedom/probability.html) of finding a quantum system in a particular state _n_. As long as this absolute value (in Dirac bra-ket notation) is finite, < _ψn | ψn_ > ≡ ∫ _ψ* (q) ψ (q) dq_ < ∞,         (2) then _ψ_ can be normalized, so that the probability of finding a particle somewhere < _ψ | ψ_ > = 1, which is necessary for its interpretation as a probability. The normalized wave function can then be used to calculate "observables" like the energy, momentum, etc. For example, the probable or expectation value for the position _r_ of the system, in configuration space _q_, is < _ψ | r | ψ_ > = ∫ _ψ* (q) r ψ (q) dq_.         (3) 2. _The Principle of Superposition_. The Schrōdinger equation (1) is a _linear_ equation. It has no quadratic or higher power terms, and this introduces a profound - and for many scientists and philosophers a disturbing - feature of quantum mechanics, one that is _impossible in classical physics_, namely the principle of superposition of quantum states. If _ψa_ and _ψb_ are both solutions of equation (1), then an arbitrary linear combination of these, | _ψ_ > = ca | _ψa_ > + cb | _ψb_ >,         (4) with complex coefficients ca and cb, is also a solution. Together with Born's probabilistic (statistical) interpretation of the wave function, the principle of superposition accounts for the major mysteries of quantum theory, some of which we hope to resolve, or at least reduce, with an objective (observer-independent) explanation of _irreversible_ [information creation](https://www.informationphilosopher.com/introduction/physics/interpretations/introduction/creation/) during quantum processes. Observable information is critically necessary for measurements, though observers can come along anytime after the information comes into existence as a consequence of the interaction of a quantum system and a measuring apparatus. The quantum (discrete) nature of physical systems results from there generally being a large number of solutions _ψn_ (called eigenfunctions) of equation (1) in its time independent form, with energy eigenvalues _En_. _H ψn_ = _En ψn_,         (5) The discrete spectrum energy eigenvalues _En_ limit interactions (for example, with photons) to specific energy differences _En_ - _Em_. In the old quantum theory, Bohr postulated that electrons in atoms would be in "stationary states" of energy _En_, and that energy differences would be of the form _En_ - _Em_ = _hν_, where _ν_ is the frequency of the observed spectral line. Einstein, in 1916, _derived_ these two Bohr postulates from basic physical principles in his paper on the emission and absorption processes of atoms. What for Bohr were assumptions, Einstein grounded in quantum physics, though virtually no one appreciated his foundational work at the time, and few appreciate it today, his work eclipsed by the Copenhagen physicists. The eigenfunctions _ψn_ are orthogonal to each other < _ψn | ψm_ > = δnm         (6) where the "delta function" δnm = 1, if _n = m_, and = 0, if _n ≠ m_.         (7) Once they are normalized, the _ψn_ form an orthonormal set of functions (or vectors) which can serve as a basis for the expansion of an arbitrary wave function _φ_  | _φ_ > = ∑ n = 0 n = ∞ _cn_ | _ψn_ >.         (8) The expansion coefficients are _cn_ = < _ψn_ | _φ_ >.         (9) In the abstract Hilbert space, < _ψn_ | _φ_ > is the "projection" of the vector _φ_ onto the orthogonal axes _ψn_ of the _ψn_ "basis" vector set. 2.1 An example of superposition. Dirac tells us that a diagonally polarized photon can be represented as a _superposition_ of vertical and horizontal states, with complex number coefficients that represent "_probability amplitudes_." Horizontal and vertical polarization eigenstates are the only "_possibilities_," if the measurement apparatus is designed to measure for horizontal or vertical polarization. 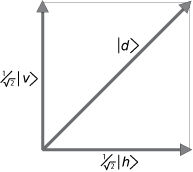Thus, | _d_ > = ( 1/√2) | _v_ > + ( 1/√2) | _h_ >          (10)  The vectors (wave functions) _v_ and _h_ are the appropriate choice of basis vectors, the vector lengths are normalized to unity, and the sum of the squares of the probability amplitudes is also unity. This is the orthonormality condition needed to interpret the (squares of the) wave functions as _probabilities_. When these (in general complex) number coefficients (1/√2) are squared (actually when they are multiplied by their complex conjugates to produce positive real numbers), the numbers (1/2) represent the probabilities of finding the photon in one or the other state, should a measurement be made on an initial state that is diagonally polarized. Note that if the initial state of the photon had been vertical, its projection along the vertical basis vector would be unity, its projection along the horizontal vector would be zero. Our probability predictions then would be - vertical = 1 (certainty), and horizontal = 0 (also certainty). Quantum physics is not always [uncertain](https://www.informationphilosopher.com/freedom/uncertainty.html), despite its reputation. 3. _The Axiom of Measurement_. The axiom of measurement depends on the idea of "observables," physical quantities that can be measured in experiments. A physical observable is represented as an operator _A_ that is "Hermitean" (one that is "self-adjoint" - equal to its complex conjugate, _A* = A_). The diagonal _n, n_ elements of the operator's matrix, < _ψn | A | ψn_ > = ∫ ∫ _ψ* (q) A (q) ψ (q) dq_,         (11) are interpreted as giving the expectation value for _An_ (when we make a measurement). The molecule suffers a recoil in the amount of _hν/c_ during this elementary process of emission of radiation; the direction of the recoil is, at the present state of theory, determined by "chance"... The weakness of the theory is, on the one hand, that it does not bring us closer to a link-up with the wave theory; on the other hand, it also leaves time of occurrence and direction of the elementary processes a matter of "chance." It speaks in favor of the theory that the statistical law assumed for [spontaneous] emission is nothing but the Rutherford law of radioactive decay. [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/), 1916 The off-diagonal _n, m_ elements describe the uniquely quantum property of interference between wave functions and provide a measure of the probabilities for transitions between states _n_ and _m_. It is the intrinsic quantum _probabilities_ that provide the ultimate source of [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html), and consequently of irreducible irreversibility, as we shall see. Transitions between states are irreducibly random, like the decay of a radioactive nucleus (discovered by Rutherford in 1901) or the emission of a photon by an electron transitioning to a lower energy level in an atom (explained by Einstein in 1916). The axiom of measurement is the formalization of Bohr's 1913 postulate that atomic electrons will be found in stationary states with energies _En_. In 1913, Bohr visualized them as orbiting the nucleus. Later, he said they could not be visualized, but chemists routinely visualize them as clouds of probability amplitude with easily calculated shapes that correctly predict chemical bonding. The off-diagonal transition probabilities are the formalism of Bohr's "quantum jumps" between his stationary states, emitting or absorbing energy _hν_ = _En_ - _Em_. Einstein explained clearly in 1916 that the jumps are accompanied by his discrete light quanta (photons), but Bohr continued to insist that the radiation was classical for another ten years, deliberately ignoring Einstein's foundational efforts in what Bohr might have felt was his area of expertise (quantum mechanics). The axiom of measurement asserts that a large number of measurements of the observable _A_, known to have eigenvalues _An_, will result in the number of measurements with value _An_ that is proportional to the probability of finding the system in eigenstate _ψn_. Quantum mechanics is a probabilistic and statistical theory. The _probabilities_ are theories about what experiments will show. Experiments provide the _statistics_ (the frequency of outcomes) that confirm the predictions of quantum theory - with the highest accuracy of any theory ever discovered! 4. _The Projection Postulate_. The third novel idea of quantum theory is often considered the most radical. It has certainly produced some of the most radical ideas ever to appear in physics, in attempts by various "interpretations" to deny it. The projection postulate is actually very simple, and arguably intuitive as well. It says that when a measurement is made, the system of interest will be found in (will instantly "collapse" into) one of the possible eigenstates of the measured observable. We have several _possibilities_ for eigenvalues. We can calculate the _probabilities_ for each eigenvalue. Measurement simply makes one of these _actual_, and it does so, said Max Born, in proportion to the absolute square of the probability amplitude wave function _ψn_. Note that [Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) saw the chance in quantum theory at least ten years before Born In this way, ontological chance enters physics, and it is partly this fact of quantum randomness that bothered Einstein ("God does not play dice") and Schrōdinger (whose equation of motion for the probability-amplitude wave function is deterministic). The projection postulate, or collapse of the wave function, is the element of quantum mechanics most often denied by various "interpretations." The sudden discrete and discontinuous "quantum jumps" are considered so non-intuitive that interpreters have replaced them with the most outlandish (literally) alternatives. The famous "many-worlds interpretation" substitutes a "splitting" of the entire universe into two equally large universes, massively violating the most fundamental conservation principles of physics, rather than allow a diagonal photon arriving at a polarizer to suddenly "collapse" into a horizontal or vertical state. 4.1 _An example of projection_. Given a quantum system in an initial state | _φ_ >, we can expand it in a linear combination of the eigenstates of our measurement apparatus, the | _ψn_ >. | _φ_ > = ∑ n = 0 n = ∞ _cn_ | _ψn_ >.         (8) In the case of [Dirac's polarized photons](https://www.informationphilosopher.com/solutions/experiments/dirac_3-polarizers/), the diagonal state | _d_ > is a linear combination of the horizontal and vertical states of the measurement apparatus, | _v_ > and | _h_ >. When we square the (1/√2) coefficients, we see there is a 50% chance of measuring the photon as either horizontal or vertically polarized. | _d_ > = ( 1/√2) | _v_ > + ( 1/√2) | _h_ >          (10) 4.2 _Visualizing projection_. When a photon is prepared in a vertically polarized state | _v_ >, its interaction with a vertical polarizer is easy to visualize. We can picture the state vector of the whole photon simply passing through the polarizer unchanged. The same is true of a photon prepared in a horizontally polarized state | _h_ > going through a horizontal polarizer. And the interaction of a horizontal photon with a vertical polarizer is easy to understand. The vertical polarizer will absorb the horizontal photon completely. The diagonally polarized photon | _d_ >, however, fully reveals the non-intuitive nature of quantum physics. We can visualize quantum [indeterminacy](https://www.informationphilosopher.com/freedom/indeterminacy.html), its [statistical](https://www.informationphilosopher.com/freedom/probability.html) nature, and we can dramatically visualize the process of [collapse](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/), as a state vector aligned in one direction must rotate instantaneously into another vector direction.  As we saw above (Figure 2.1), the vector projection of | _d_ > onto | _v_ >, with length (1/√2), gives us the probability 1/2 for photons to emerge from the vertical polarizer. But this is only a statistical statement about the expected probability for large numbers of identically prepared photons. When we have only one photon at a time, _we never get one-half of a photon_ coming through the polarizer. Critics of standard quantum theory sometimes say that it tells us nothing about individual particles, only ensembles of identical experiments. There is truth in this, but nothing stops us from imagining the strange process of a single diagonally polarized photon interacting with the vertical polarizer. There are two possibilities. We either get a whole photon coming through (which means that it "collapsed" or the diagonal vector was "reduced to" a vertical vector) or we get no photon at all. This is the entire meaning of "collapse." It is the same as an atom "jumping" discontinuously and suddenly from one energy level to another. It is the same as the photon in a two-slit experiment suddenly appearing at one spot on the photographic plate, where an instant earlier it might have appeared anywhere. We can even visualize what happens when no photon appears. We can imagine that the diagonal photon was reduced to a horizontally polarized photon and was completely absorbed. Why can we see the statistical nature and the indeterminacy? First, statistically, in the case of many identical photons, we can say that half will pass through and half will be absorbed. The indeterminacy is that in the case of one photon, we have no ability to know which it will be. This is just as we cannot predict the time when a radioactive nucleus will decay, or the time and direction of an atom emitting a photon. This indeterminacy is a consequence of our diagonal photon state vector being "represented" (transformed) into a linear superposition of vertical and horizontal photon state vectors. Thus the _principle of superposition_ together with the _projection postulate_ provides us with indeterminacy, statistics, and a way to "visualize" the collapse of a superposition of quantum states into one of the basis states.