# Schrödinger's Cat [Erwin Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger)'s intention for his infamous cat-killing box was to discredit certain non-intuitive implications of quantum mechanics, of which his wave mechanics was the second formulation. Schrödinger's wave mechanics is more continuous mathematically, and _apparently_ more [deterministic](https://www.informationphilosopher.com/freedom/determinism.html), than [Werner Heisenberg](https://www.informationphilosopher.com/solutions/scientists/heisenberg/)'s matrix mechanics. Schrödinger did not like [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr)'s idea of "quantum jumps" between Bohr's "stationary states" - the different "energy levels" in an atom. Bohr's "quantum postulate" said that the jumps between discrete states emitted (or absorbed) energy in the amount hν = E2 - E1. Bohr did not accept [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein)'s 1905 hypothesis that the radiation was a spatially localized quantum of energy hν. Until well into the 1920's, Bohr (and [Max Planck](https://www.informationphilosopher.com/solutions/scientists/planck), the inventor of the quantum hypothesis himself) believed radiation was a continuous wave. This was the question of [wave-particle duality](https://www.informationphilosopher.com/introduction/physics/wave-particle_duality.html), which Einstein saw as early as 1909. It was Einstein who originated the suggestion that the superposition of Schrödinger's wave functions implied that two different physical states could exist at the same time. This was a serious interpretational error that plagues the foundation of quantum physics to this day. This error is found frequently in discussions of so-called "[entangled](https://www.informationphilosopher.com/problems/entanglement/)" states (see the [Einstein-Podolsky-Rosen](https://www.informationphilosopher.com/solutions/experiments/EPR/) experiment). Entanglement occurs only for atomic level phenomena and over limited distances that preserve the coherence of two-particle wave functions by isolating the systems (and their eigenfunctions) from interactions with the environment. We never actually "see" or measure any system (whether a microscopic electron or a macroscopic cat) in two distinct states. Quantum mechanics simply predicts a significant probability of the system being found in these different states. And these probability predictions are borne out by the statistics of large numbers of identical experiments. > The [Pauli](https://www.informationphilosopher.com/solutions/scientists/pauli) Exclusion Principle says (correctly) that two identical indistinguishable (fermion) particles cannot be in the same place at the same time. Entanglement is often interpreted (incorrectly) as saying that a single particle can be in two places at the same time. [Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac)'s Principle of Superposition does not say that a particle _**is** in two states_ at the same time, only that there is a non-zero probability of finding it in either state should it be measured. [Max Born](https://www.informationphilosopher.com/solutions/scientists/born) described the somewhat paradoxical result: > The motion of the particle follows the laws of probability, but the probability itself propagates in accord with causal laws. Einstein wrote to Schrödinger with the idea that the decay of a radioactive nucleus could be arranged to set off a large explosion. Since the moment of decay is unknown, Einstein argued that the superposition of decayed and undecayed nuclear states implies the superposition of an explosion and no explosion. It does not. In both the microscopic and macroscopic cases, quantum mechanics simply estimates the probability amplitudes for the two cases. Many years later, [Richard Feynman](https://www.informationphilosopher.com/solutions/scientists/feynman) made Einstein's suggestion into a nuclear explosion! (What is it about some scientists?) Einstein and Schrödinger did not like the fundamental randomness implied by quantum mechanics. They wanted to restore determinism to physics. Indeed Schrödinger's wave equation predicts a perfectly deterministic time evolution of the wave function. But what is evolving deterministically is only abstract probabilities. And these probabilities are confirmed only in the statistics of large numbers of identically prepared experiments. Randomness enters only when a [measurement](https://www.informationphilosopher.com/problems/measurement/) is made and the [wave function "collapses"](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) into one of the possible states of the system. Schrödinger devised a variation in which the random radioactive decay would kill a cat. Observers could not know what happened until the box is opened. The details of the tasteless experiment include: - a [Geiger counter](https://www.informationphilosopher.com/solutions/experimants/geiger_counter/) which produces an avalanche of electrons when an alpha particle passes through it - a bit of radioactive material with a decay half-life likely to emit an alpha particle in the direction of the Geiger counter during a time _T_ - an electrical circuit energized by the electrons which drops a hammer - a flask of a deadly hydrocyanic acid gas, smashed open by the hammer. The gas will kill the cat, but the exact time of death is unpredictable and random because of the irreducible quantum indeterminacy in the time of decay (and the direction of the decay particle, which might miss the Geiger counter!). This thought experiment is widely misunderstood. It was meant (by both Einstein and Schrödinger) to suggest that quantum mechanics describes the simultaneous (and obviously contradictory) existence of a live and dead cat. Here is the famous diagram with a cat both dead and alive.  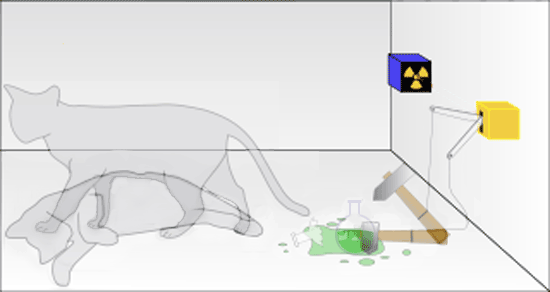## What's wrong with this picture? Quantum mechanics claims only that the time evolution of the Schrödinger wave functions for the probability amplitudes of nuclear decay accurately predict the proportion of nuclear decays that will occur in a given time interval. (Classical) probabilities (no interference between terms) simply predict the number of live and dead cats that will be observed in a large number of identical experiments. Quantum "probability amplitudes" do allow interference between the possible states of a quantum object, but not between macroscopic objects like live and dead cats More specifically, quantum mechanics provides us with the accurate prediction that if this experiment is repeated many times (the SPCA would disapprove), half of the experiments will result in dead cats. Note that this is a problem in [epistemology](https://www.informationphilosopher.com/knowledge/). What knowledge is it that quantum physics provides? 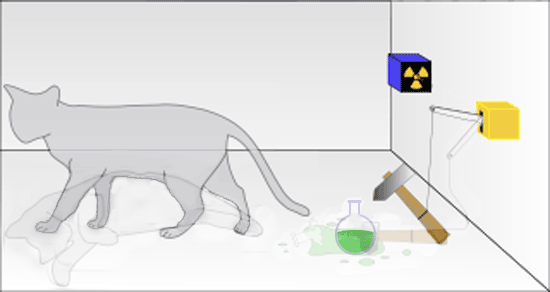If we open the box at the time _T_ when there is a 50% probability of an alpha particle emission, the most a physicist can know is that there is a 50% chance that the radioactive decay will have occurred and the cat will be observed as dead or dying. If the box were opened earlier, say at _T/2_, there is only a 25% chance that the cat has died. Schrödinger's superposition of live and dead cats would look like this.  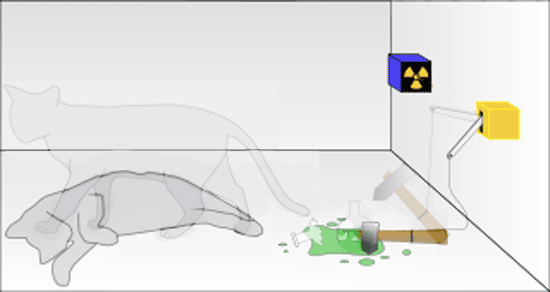If the box were opened later, say at _2T_, there is only a 25% chance that the cat is still alive. Quantum mechanics is giving us only statistical information - knowledge about probabilities.  Schrödinger is simply wrong that the mixture of nuclear wave functions that accurately describes decay can be magnified to the macroscopic world to describe a similar mixture of live cat and dead cat wave functions and the simultaneous existence of live and dead cats. The kind of coherent _superposition of states_ needed to describe an atomic system as in a linear combination of states (see Paul Dirac's explanation of superposition using [three polarizers](https://www.informationphilosopher.com/solutions/experiments/dirac_three-polarizers/)) does not describe macroscopic systems. Instead of a linear combination of pure quantum states, with quantum interference between the states, i.e., | _Cat_ > = ( 1/√2) | _Live_ > + ( 1/√2) | _Dead_ >, quantum mechanics tells us only that there is 50% chance of finding the cat in either the live or dead state, i.e., _Cats_ = (1/2) _Live_ + (1/2) _Dead_. Just as in the quantum case, this probability prediction is confirmed by the statistics of repeated identical experiments, but no interference between these states is seen. What do exist simultaneously in the macroscopic world are genuine [alternative possibilities](https://www.informationphilosopher.com/freedom/alternative_possibilities.html) for future events. There is the real possibility of a live or dead cat in any particular experiment. Which one is found is irreducibly random, unpredictable, and a matter of pure [chance](https://www.informationphilosopher.com/freedom/chance.html). Genuine [alternative possibilities](https://www.informationphilosopher.com/freedom/alternative_possibilities.html) is what bothered physicists like Einstein, Schrödinger, and [Max Planck](https://www.informationphilosopher.com/solutions/scientists/planck) who wanted a return to deterministic physics. It also bothers [determinist](https://www.informationphilosopher.com/freedom/determinism.html) and [compatibilist](https://www.informationphilosopher.com/freedom/compatibilism.html) philosophers who have what [William James](https://www.informationphilosopher.com/solutions/philosophers/james) calls an "antipathy to [chance](https://www.informationphilosopher.com/freedom/chance.html)." Ironically, it was Einstein himself, in 1916, who discovered the existence of irreducible chance, in the elementary interactions of matter and radiation. Until the information comes into existence, the future is indeterministic. Once information is macroscopically encoded, the past is determined. ## How does information physics resolve the paradox? As soon as the alpha particle sets off the avalanche of electrons in the Geiger counter (an irreversible event with a significant entropy increase), _new [information](https://www.informationphilosopher.com/introduction/information/) is created in the world_. For example, a simple pen-chart recorder attached to the Geiger counter could record the time of decay, which a human observer could read at any later time. Notice that, as usual in information creation, the energy expended by a recorder increases the entropy more than the increased information decreases it, thus satisfying the second law of thermodynamics.  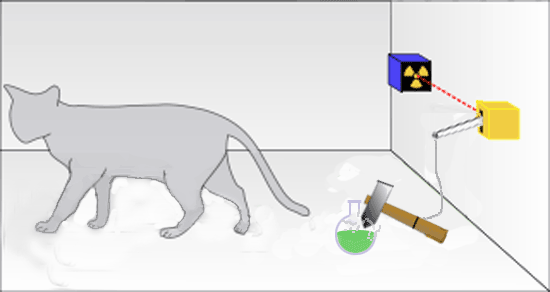Even without a mechanical recorder, the cat's death sets in motion biological processes that constitute an equivalent, if gruesome, recording. When a dead cat is the result, a sophisticated autopsy can provide an approximate time of death, because the cat's body is acting as an event recorder. There never is a superposition (in the sense of the simultaneous existence) of live and dead cats. The paradox points clearly to the Information Philosophy solution to the [problem of measurement](https://www.informationphilosopher.com/problems/measurement). Human observers are not required to make measurements. In this case, the cat is the observer. In most physics measurements, the new information is captured by apparatus well before any physicist has a chance to read any dials or pointers that indicate what happened. Indeed, in today's high-energy particle interaction experiments, the data may be captured but not fully analyzed until many days or even months of computer processing establishes what was observed. In this case, the experimental apparatus is the observer. And, in general, _the universe is its own observer_, able to record (and sometimes preserve) the information created. --- The basic assumption made in Schrödinger's cat thought experiments is that the deterministic Schrödinger equation describing a _microscopic_ superposition of decayed and non-decayed radioactive nuclei evolves [deterministically](https://www.informationphilosopher.com/solutions/experiments/schrodingerscat/freedom/determinism.html) into a _macroscopic_ superposition of live and dead cats. But since the essence of a "measurement" is an interaction with another system (quantum or classical) that creates [information](https://www.informationphilosopher.com/introduction/information/) to be seen (later) by an observer, the interaction between the nucleus and the cat is more than enough to [collapse the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). Calculating the probabilities for that collapse allows us to estimate the probabilities of live and dead cats. These are probabilities, not probability amplitudes. They do not interfere with one another. After the interaction, they are not in a superposition of states. We always have _either_ a live cat or a dead cat, just as we always observe a complete photon after [a polarization measurement](https://www.informationphilosopher.com/solutions/experiments/dirac_3-polarizers/) and not a superposition of photon states, as [P.A.M.Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac) explains so simply and clearly. > According to quantum mechanics the result of this experiment will be that sometimes one will find a whole photon, of energy equal to the energy of the incident photon, on the back side and other times one will find nothing. When one finds a whole photon, it will be polarized perpendicular to the optic axis. One will never find only a part of a photon on the back side. If one repeats the experiment a large number of times, one will find the photon on the back side in a fraction sin2α of the total number of times.  > > Quantum mechanics similarly gives us only the _probability_ of finding live cats (or dead cats) in a large number of identically prepared experiments (_pace_ the SPCA) > > Thus we may say that the photon has a probability sin2α of passing through the tourmaline and appearing on the back side polarized perpendicular to the axis and a probability cos2α of being absorbed. These values for the probabilities lead to the correct classical results for an incident beam containing a large number of photons. > > In this way we preserve the individuality of the photon in all cases. We are able to do this, however, only because we abandon the determinacy of the classical theory. The result of an experiment is not determined, as it would be according to classical ideas, by the conditions under the control of the experimenter. The most that can be predicted is a set of possible results, with a probability of occurrence for each... > > When we make the photon meet a tourmaline crystal, we are subjecting it to an observation. We are observing whether it is polarized parallel or perpendicular to the optic axis. The effect of making this observation is to force the photon entirely into the state of parallel or entirely into the state of perpendicular polarization. It has to make a sudden jump from being partly in each of these two states to being entirely in one or other of them. Which of the two states it will jump into cannot be predicted, but is governed only by probability laws. If it jumps into the parallel state it gets absorbed and if it jumps into the perpendicular state it passes through the crystal and appears on the other side preserving this state of polarization. > > Superposition and Indeterminacy > > The non-classical nature of the superposition process is brought out clearly if we consider the superposition of two states, _A_ and _B_, such that there exists an observation which, when made on the system in state _A_, is certain to lead to one particular result, _a_ say, and when made on the system in state _B_ is certain to lead to some different result, _b_ say. What will be the result of the observation when made on the system in the superposed state? The answer is that the result will be sometimes _a_ and sometimes _b_, according to a probability law depending on the relative weights of _A_ and _B_ in the superposition process. It will never be different from both _a_ and _b_.  > > There is no justification for assuming an intermediate (and absurd) condition of simultaneous live and dead cats. The thing that is "intermediate" is the probability, not the outcome. > > _The intermediate character of the state formed by superposition thus expresses itself through the probability of a particular result for an observation being intermediate between the corresponding probabilities for the original states,† not through the result itself being intermediate between the corresponding results for the original states._ > > > † The probability of a particular result for the state formed by superposition is not always intermediate between those for the original states in the general case when those for the original states are not zero or unity, so there are restrictions on the 'intermediateness' of a state formed by superposition. > > In this way we see that such a drastic departure from ordinary ideas as the assumption of superposition relationships between the states is possible only on account of the recognition of the importance of the disturbance accompanying an observation and of the consequent indeterminacy in the result of the observation. When an observation is made on any atomic system that is in a given state, in general the result will not be determinate, i.e., if the experiment is repeated several times under identical conditions several different results may be obtained. It is a law of nature, though, that if the experiment is repeated a large number of times, each particular result will be obtained in a definite fraction of the total number of times, so that there is a definite _probability_ of its being obtained. This probability is what the theory sets out to calculate. > > > (_[The Principles of Quantum Mechanics](https://www.informationphilosopher.com/solutions/scientists/dirac/chapter_1.html)_, chapter 1, pp.5-14) ## Decoherence and the Lack of Macroscopic Superpositions Despite the claims of [decoherence](https://www.informationphilosopher.com/knowledge/decoherence.html) theorists, microscopic superpositions of quantum states do not allow us to "see" a system in two different states. Quantum mechanics simply predicts a significant probability of the system being found in these different states. Thus it is no surprise that we do not see _macroscopic_ "superpositions of live and dead cats" at the same time. What does exist at any given time is the probabilities of the two states (in the macroscopic world) and the _probability amplitude_ of the two states (which can coherently interfere with one another) in the microscopic world. Decoherence theorists claim that they explain the "mysterious" non-appearance of macroscopic superpositions of states. But quantum mechanics does not predict such states, despite the popular idea of macroscopic superposition of live and dead cats. ## An Historical Note This was not Schrödinger's original idea. It was a version of an idea of Einstein's about gunpowder that could be in two quantum states. He sent this to Schrödinger in 1935... > The system is a substance in chemically unstable equilibrium, perhaps a charge of gunpowder that, by means of intrinsic forces, can spontaneously combust, and where the average life span of the whole setup is a year. In principle this can quite easily be represented quantum-mechanically. In the beginning the psi-function characterizes a reasonably well-defined macroscopic state. But, according to your equation [i.e., the Schrödinger equation], after the course of a year this is no longer the case. Rather, the psi-function then describes a sort of blend of not-yet and already-exploded systems. Through no art of interpretation can this psi-function be turned into an adequate description of a real state of affairs; in reality there is no intermediary between exploded and not-exploded.  Schrödinger turned the gunpowder into his Cat.