# The Principle of Superposition The Schrōdinger equation is _H ψn_ = _Enψn_,         (1) where H is the Hamiltonian operator, _ψn_ is the wave function for state _n_, and the _En_ are the energy eigenvalues for the states. The eigenfunctions _ψn_ are orthogonal to each other < _ψn | ψm_ > = δnm         (2) where the "delta function" δnm = 1, if _n = m_, and = 0, if _n ≠ m_.         (3) Once they are normalized, the _ψn_ form an orthonormal set of functions (or vectors) which can serve as a basis for the expansion of an arbitrary wave function _φ_  | _φ_ > = ∑ n = 0 n = ∞ _cn_ | _ψn_ >.         (4) The expansion coefficients are _cn_ = < _ψn_ | _φ_ >.         (5) In the abstract Hilbert space, < _ψn_ | _φ_ > is the "projection" of the vector _φ_ onto the orthogonal axes _ψn_ of the _ψn_ "basis" vector set. The Schrōdinger equation is a _linear_ equation. It has no quadratic or higher power terms, and this introduces the principle of _superposition_ of quantum states, a profound - and for many scientists and philosophers a disturbing - feature of quantum mechanics, one that is _impossible in classical physics_. If _ψa_ and _ψb_ are both solutions of equation (1), then an arbitrary linear combination of these, | _ψ_ > = ca | _ψa_ > + cb | _ψb_ >,         (6) with complex coefficients ca and cb, is also a solution. Born's rule, that waves are probabilities, was actually first suggested by Einstein Together with Born's probabilistic (statistical) interpretation of the wave function, the principle of superposition accounts for the major mysteries of quantum theory, some of which we hope to resolve, or at least reduce, with an objective (observer-independent) explanation of _irreversible_ [information creation](https://www.informationphilosopher.com/quantum/superposition/introduction/creation/) during quantum processes. Observable information is critically necessary for measurements, though observers can come along anytime after the information comes into existence as a consequence of the interaction of a quantum system and a measuring apparatus. The quantum (discrete) nature of physical systems results from there generally being a large number of solutions _ψn_ (called eigenfunctions) of equation (1) in its time independent form, with energy eigenvalues _En_. An example of superposition. Dirac tells us that a diagonally polarized photon can be represented as a _superposition_ of vertical and horizontal states, with complex number coefficients that represent "_probability amplitudes_." Horizontal and vertical polarization eigenstates are the only "_possibilities_," if the measurement apparatus is designed to measure for horizontal or vertical polarization. 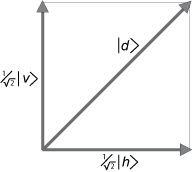Thus, | _d_ > = ( 1/√2) | _v_ > + ( 1/√2) | _h_ >          (10)  The vectors (wave functions) _v_ and _h_ are the appropriate choice of basis vectors, the vector lengths are normalized to unity, and the sum of the squares of the probability amplitudes is also unity. This is the orthonormality condition needed to interpret the (squares of the) wave functions as _probabilities_. When these (in general complex) number coefficients (1/√2) are squared (actually when they are multiplied by their complex conjugates to produce positive real numbers), the numbers (1/2) represent the probabilities of finding the photon in one or the other state, should a measurement be made on an initial state that is diagonally polarized. Note that if the initial state of the photon had been vertical, its projection along the vertical basis vector would be unity, its projection along the horizontal vector would be zero. Our probability predictions then would be - vertical = 1 (certainty), and horizontal = 0 (also certainty). Quantum physics is not always [uncertain](https://www.informationphilosopher.com/freedom/uncertainty.html), despite its reputation.