# The Two-Slit Experiment and "One Mystery" of Quantum Mechanics [Richard Feynman](https://www.informationphilosopher.com/solutions/scientists/feynman) said that the two-slit experiment contains the "one mystery" of quantum mechanics. > I will take just this one experiment, which has been designed to contain all of the mystery of quantum mechanics, to put you up against the paradoxes and mysteries and peculiarities of nature one hundred per cent. Any other situation in quantum mechanics, it turns out, can always be explained by saying, 'You remember the case of the experiment with the two holes? It's the same thing'. > > > [_The Character of Physical Law, chapter 6_](https://www.informationphilosopher.com/solutions/scientists/feynman/probability_and_uncertainty.htm#one_mystery) We will show that the (one) mystery of quantum mechanics is how mere "probabilities" can causally control (statistically) the positions of material particles - how _immaterial information_ can affect the material world. This remains a deep _metaphysical_ mystery. The two-slit experiment was until recent years for the most part a thought experiment, since it is difficult to build an inexpensive demonstration, but its predictions have been verified in many ways since the 1960's, primarily with electrons. Recently, extremely sensitive CCDs used in photography have been used to collect single-photon events, establishing experimentally everything that [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) imagined, merely by thinking about it, as early as 1905.  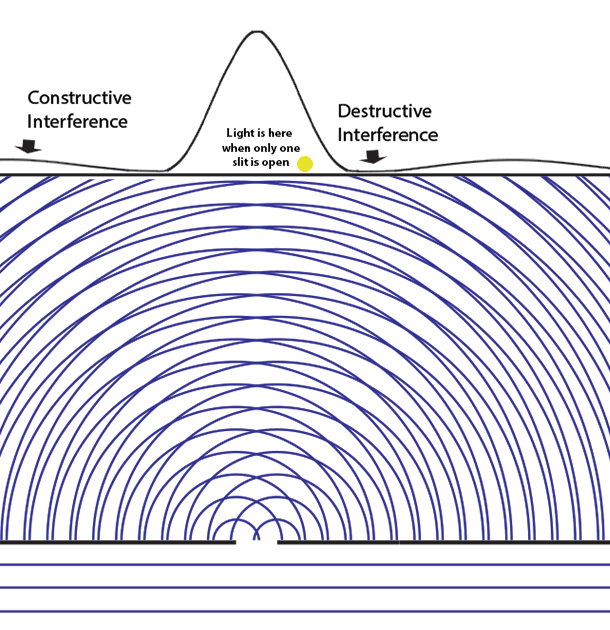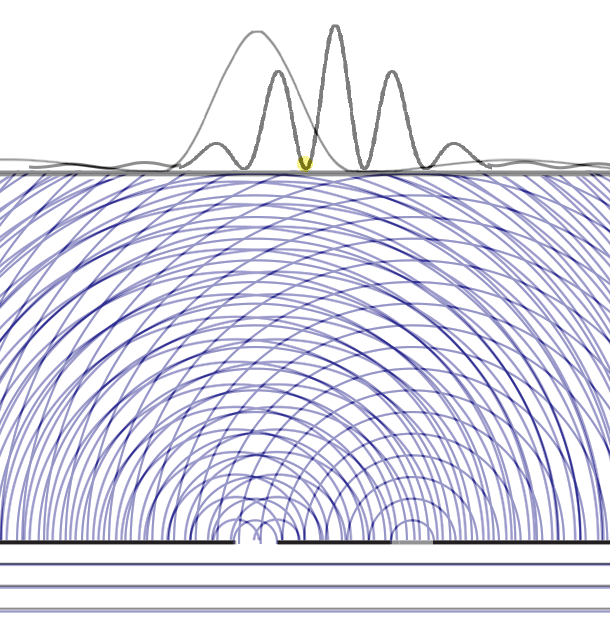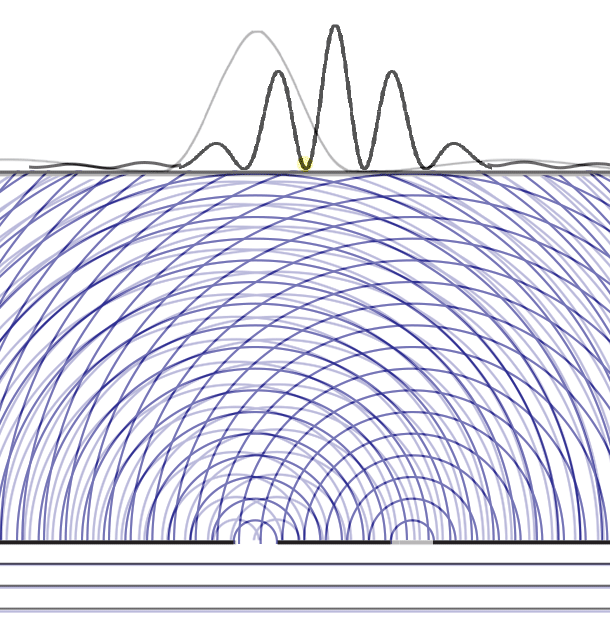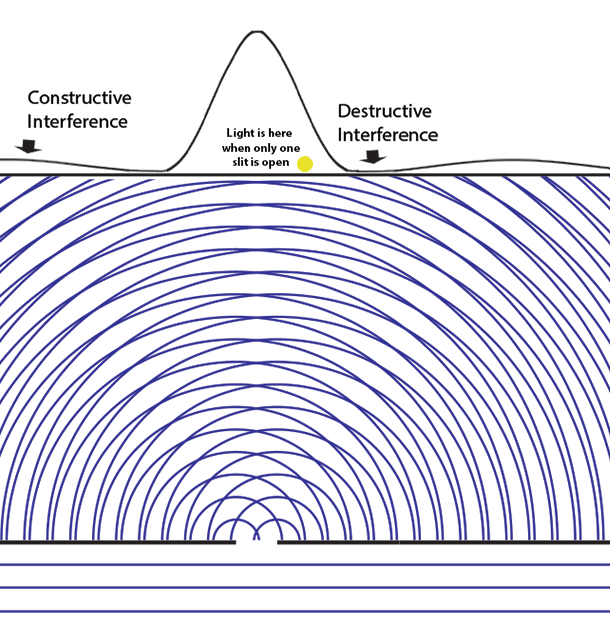Light at the yellow dot slowly disappears as the second slit opens! Adding light causes some light to disappear! The two-slit experiment demonstrates better than any other experiment that a quantum wave function ψ is a _probability amplitude_ that can _interfere with itself_, producing places where the probability |ψ|2 (the square of the absolute value of the complex probability amplitude) of finding a quantum particle is actually zero. Perhaps the most non-intuitive aspect of the two-slit experiment is when we first note the pattern of light on the screen with just one slit open, then open the second slit - admitting more light into the experiment, and observe that some places on the screen where there was visible light through on slit, have now gone dark! And this happens even when we are admitting only one particle of light at a time. How Feynman asked, can that single particle know that two slits are open? Light waves are often compared to water waves, as are quantum probability waves, but this latter is a serious error. Water waves and light waves (as well as sound waves) contain something _substantial_ like matter or energy. But quantum waves are just abstract information - mathematical possibilities. As [Paul Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/) tells us, quantum wave functions are not substances.  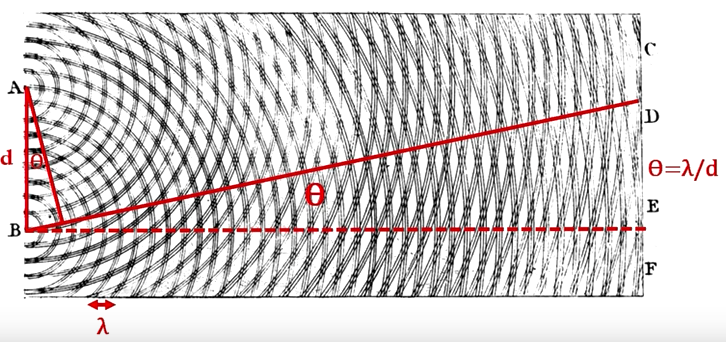Young's 1802 drawing of wave interference [Water waves in a pond](https://youtu.be/Iuv6hY6zsd0?t=268) [Dr. Quantum and the two-slit experiment](https://youtu.be/DfPeprQ7oGc) The cancellation of crests and troughs in the motion of water and other waves creates high and low points in water waves that have the same shape as bright and dark areas found in the "fringes" of light at the sharp edges of an object. These interference pattern were predicted to occur in double-slit experiments by [Thomas Young](https://en.wikipedia.org/wiki/Thomas_Young_(scientist)) in the early nineteenth century. The two-slit experiment is thought to demonstrate the famous ["collapse" of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) or "reduction" of the wave packet, which show an inherent probabilistic element in quantum mechanics that is irreducibly ontological and nothing like the epistemological indeterminacy (human ignorance) in classical statistical physics. We shall see below that the idea of the light wave "collapsing" instantaneously to become a particle was first seen by Einstein in 1905. This is a mistake, one still widely taught. Note that the probability amplitude ψ is pure [information](https://www.informationphilosopher.com/introduction/information/). It is neither matter nor energy. When a wave function "collapses" or "goes through both slits" in this dazzling experiment, nothing material or energetic is traveling faster than the speed of light or going through both slits. We argue that the particle of matter or energy always goes through just one slit, although the popular [Copenhagen interpretation](https://www.informationphilosopher.com/introduction/physics/copenhagen_interpretation.html) of physics claims we cannot know the particle path, that a path does not even exist until we make a measurement, that the particle may be in more than one place at the same time, and other similar nonsense that deeply bothered [Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) as he hoped for an "objective reality" independent of human observers. ([David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/)'s "pilot-wave theory" agrees that an objectively real particle travels through one slit, guided by its pilot wave, which travels through both.) A large number of [panpsychists](https://www.informationphilosopher.com/mind/panpsychism), some philosophers, and some scientists, believe that the [mind](https://www.informationphilosopher.com/mind/) of a [conscious observer](https://www.informationphilosopher.com/quantum/observer/) is needed to cause the [collapse of the wave function](https://www.informationphilosopher.com/quantum/collapse/). There is something similar going on in the [Einstein-Podolsky-Rosen](https://www.informationphilosopher.com/solutions/experiments/EPR/) thought experiments, where measurement of a particular spin component of one particle means that the other particle now has the exact opposite value of its same spin component, to conserve total spin zero. Nothing physical (matter or energy) is transmitted to the other "entangled" particle. The idea that an immaterial bit of information is "teleported" to the other particle is also mistaken. The anti-parallel spins are created together simultaneously, in a special frame of reference. There is no violation of relativity. We shall show that it is conservation of angular momentum or of spin that makes the state of the coherently entangled second particle determinate, however far away it might be after the measurement. In the two-slit experiment, just as in the [Dirac Three Polarizers](https://www.informationphilosopher.com/solutions/experiments/dirac_three-polarizers/) experiment, the critical case to consider is just one photon or electron at a time in the experiment. With one particle at a time (whether photon or electron), the quantum object is mistakenly described as interfering with itself, when interference is never seen in a single event. Interference only shows up in the _statistics_ of large numbers of experiments. Even in the one-slit case, interference fringes are visible when large numbers of particles are present, although this is rarely described in the context of the [two-slit quantum mystery](https://www.informationphilosopher.com/freedom/mysteries.html). It is the fundamental relation between a particle and the associated wave that controls a particle's probable location that raises the "local reality" question first seen in 1905 and described in 1909 by [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/). Thirty years later, the EPR paper and [Erwin Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger)'s insights into the wave function of two [entangled](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/problems/entanglement/) particles, first convinced physicists that there was a deep problem . It was not for another thirty years that [John Stewart Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) in 1964 imagined an experimental test that could confirm or deny quantum mechanics. Ironically, the goal of Bell's "theorem" was to invalidate the non-intuitive aspects of quantum mechanics and restore Einstein's hope for a more deterministic picture of an "objective reality" at, or perhaps even underlying below, the microscopic level of quantum physics. At about the same time, in his famous _Lectures on Physics_ at Cal Tech and the _Messenger Lectures_ at Cornell, [Richard Feynman](https://www.informationphilosopher.com/solutions/scientists/feynman/) described the two-slit experiment as demonstrating what he claimed is the "only mystery" of quantum mechanics. We can thus begin the discussion of the two-slit experiment with a section from Feynman's sixth Messenger lecture entitled "Probability and Uncertainty." We provide the complete video and text of the lecture on [this page](https://www.informationphilosopher.com/solutions/scientists/feynman/probability_and_uncertainty.html), and a version starting with Feynman's provocative statement that "no one understands quantum mechanics" below. [Open the text of the lecture in a new window so you can read along with the video](https://www.informationphilosopher.com/solutions/scientists/feynman/probability_and_uncertainty.html). How, Feynman asks, can a single particle go through both slits? Our answer (and [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/)'s) is that each particle goes though one sit, conserving matter and energy. The particle always goes through a single slit. A particle cannot be divided and in two places at the same time. It is the wave function that interferes with itself. And the highly localized particle can not be _identified_ with the wave widely distributed in space. The wave function ψ is determined by solving the Schrödinger equation given the _boundary conditions_ of the measuring apparatus (the container). We will see that the thing that goes through both slits is only _immaterial information_ - the probability amplitude wave function ψ (t) if we solve the time-dependent Schrödinger equation. The _immaterial_ wave function exerts a [causal](https://www.informationphilosopher.com/freedom/causality.html) influence over the particles, one that we can justifiably call "mysterious." It results in the statistics of many experiments agreeing with the quantum mechanical predictions. with increasing accuracy as we increase the number of identical experiments. 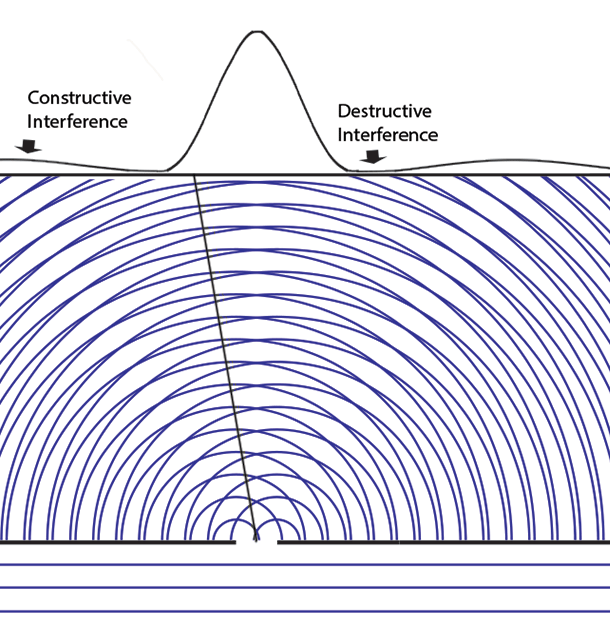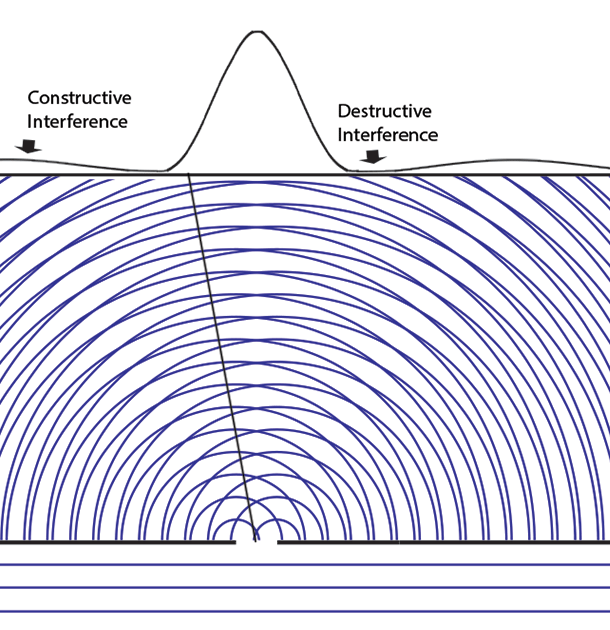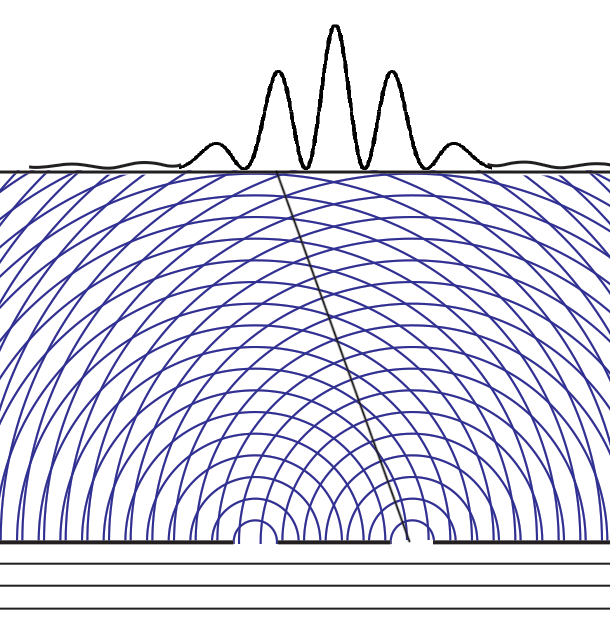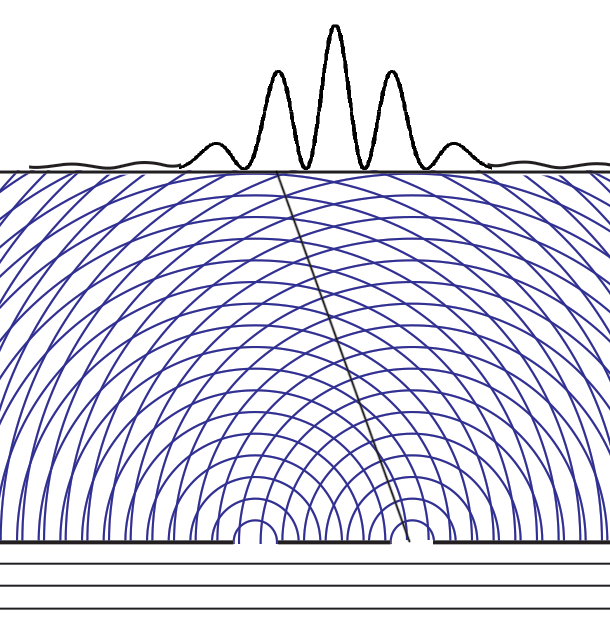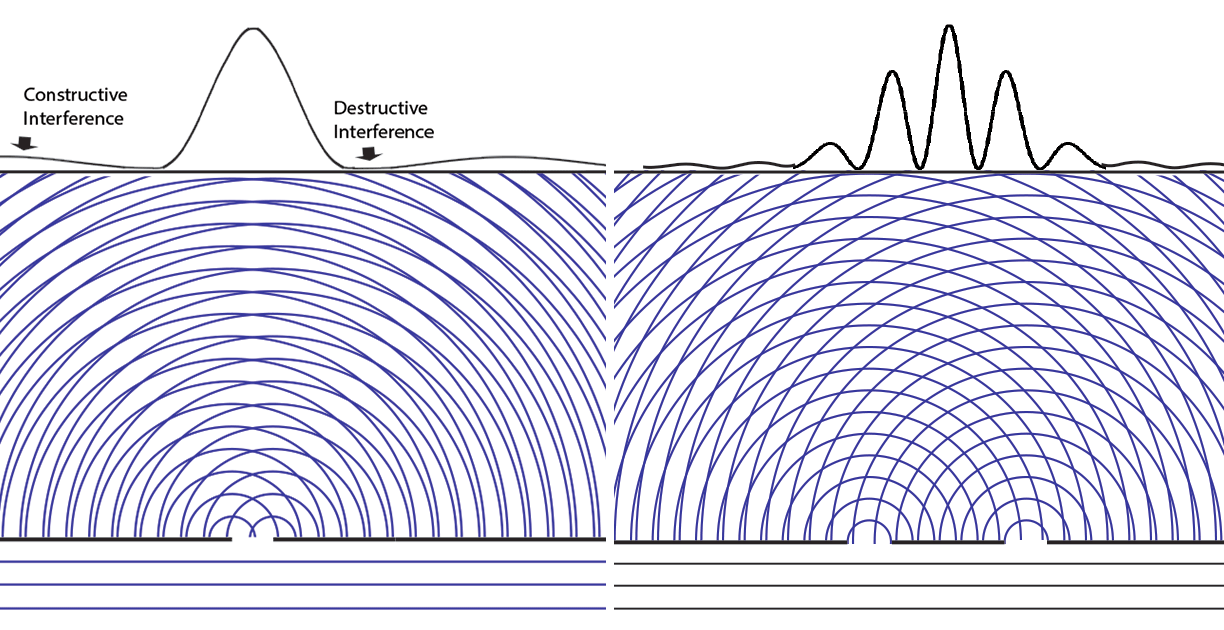_It is this "influence," no ordinary "force," that is Feynman's "only mystery" in quantum mechanics._ Let's look first at the one-slit case. We prepare a slit that is about the same size as the wavelength of the light in order to see the Fraunhofer diffraction effects most clearly. Parallel waves from a distant source fall on the slit from below. The diagram shows that the wave from the left edge of the slit interferes with the one from the right edge. If the slit width is _d_ and the photon wavelength is λ, at an angle α ≈ λ/2_d_ there will be destructive interference. At an angle α ≈ λ/_d_, there is constructive interference (which shows up as the fanning out of lightening patterns in the interfering waves in the illustration). The light constructive interference leads toward the peaks in the interference pattern.  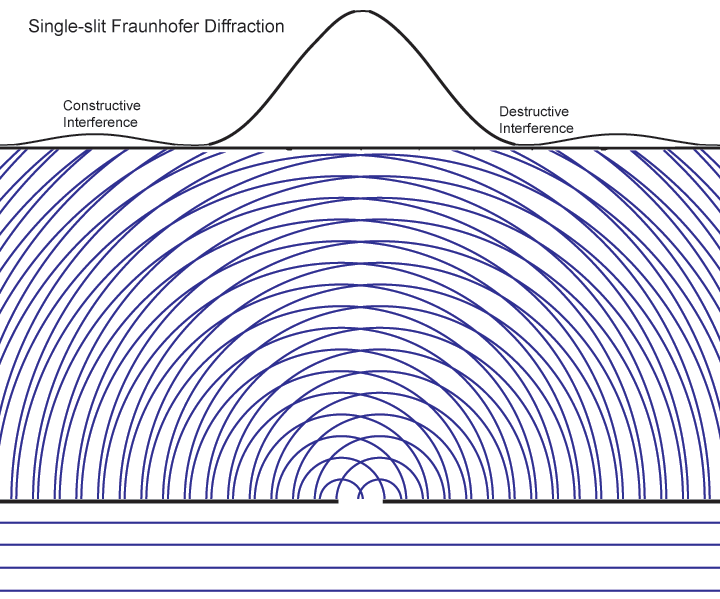The height of the function or curve on the top of the diagram is proportional to the number of photons falling along the screen. At first they are individual pixels in a CCD or grains in a photographic plate, but over time and very large numbers of photons they appear as the continuous gradients of light in the band below (we represent this intensity as the height of the function).  Now what happens if we add a second slit? Perhaps we should start by showing what happens if we run the experiment with the first slit open for a time, and then with the second slit open for an equal time. In this case, the height of the intensity curve is the sum of the curves for the individual slits.  But that is not the intensity curve we get when the two slits are open at the same time! Instead, we see many new interference fringes with much narrower width angles α ≈ λ/_D_, where _D_ is now the distance between the two slits. Note that the overall envelope of the curve is similar to that of one big slit of width _D_. And also note many more lightening fan-outs of constructive interference in the overlapping waves.  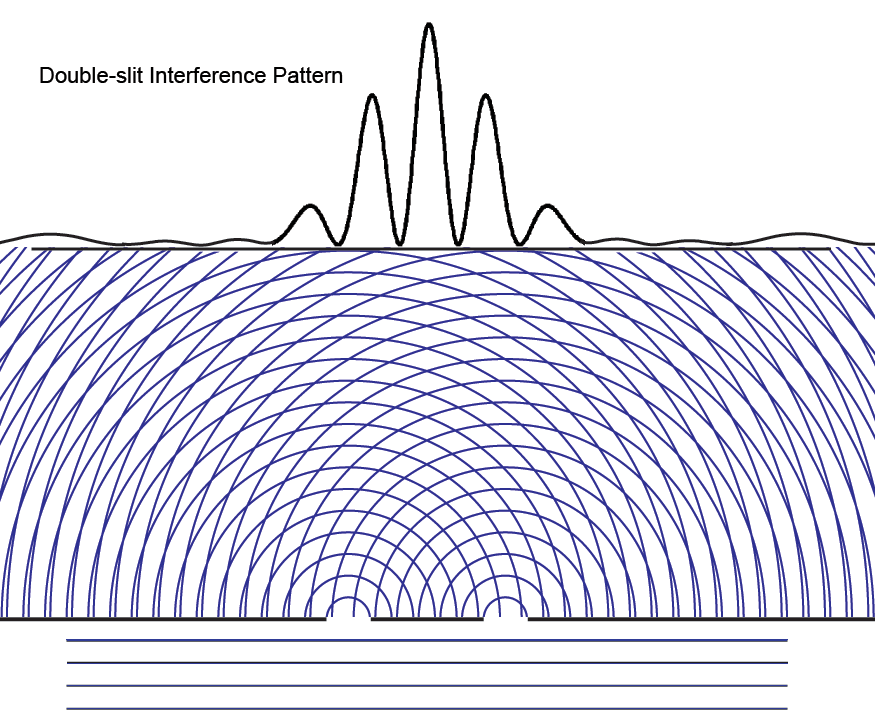Remembering that the double-slit interference appears even if _only one particle at a time_ is incident on the two slits, we see why many say that the particle interferes with itself. But it is the wave function alone that is interfering with itself. Whichever slit the particle goes through, it is the probability amplitude ψ, whose squared modulus |ψ|2 gives us the probability of finding a particle somewhere, the interference pattern. It is what it is because _the two slits are open_.  This is the deepest metaphysical mystery in quantum mechanics. How can an abstract probability wave influence the particle paths to show interference when large numbers of particles are collected? 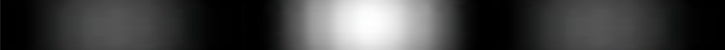**Why interference patterns show up when both slits are open, even when particles go through just one slit, though we cannot know which slit or we lose the interference** | | | |---|---| ||| || | |When there is only one slit open (here the left slit), the probabilities pattern has one large maximum (directly behind the slit) and small side fringes. If only the right slit were open, this pattern would move behind the right slit.<br><br>If we add up the results of some experiments with the left slit open and others with the right open we don't see the multiple fringes that appear with two slits open.<br><br>|When both slits are open, the maximum is now at the center between the two slits, there are more interference fringes, and these probabilities apply _whichever slit the particle enters_. The solution of the Schrödinger equation depends on the boundary conditions - different when two holes are open. The "one mystery" remains - how these "probabilities" can exercise causal control (statistically) over matter or energy particles.<br><br>Feynman's path integral formulation of quantum mechanics suggests the answer. His "virtual particles" explore all space (the "sum over paths") as they determine the variational minimum for least action, thus the resulting probability amplitude wave function can be said to "know" which holes are open.| Now let's slow down the opening and closing of the right-hand slit so we can see more closely what's happening.  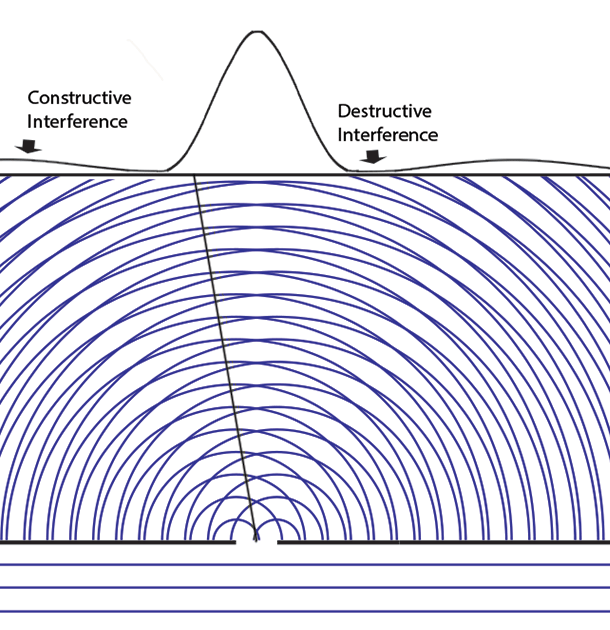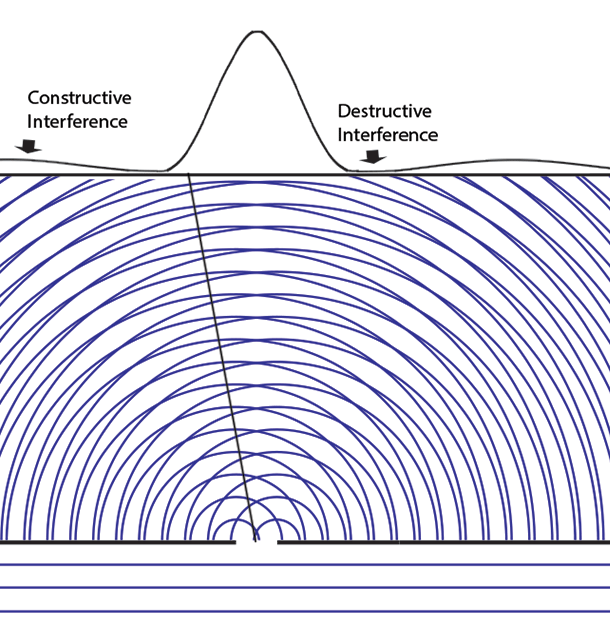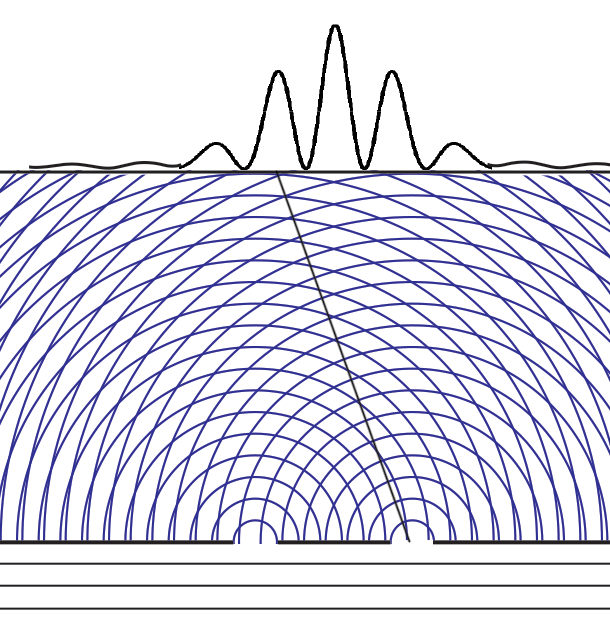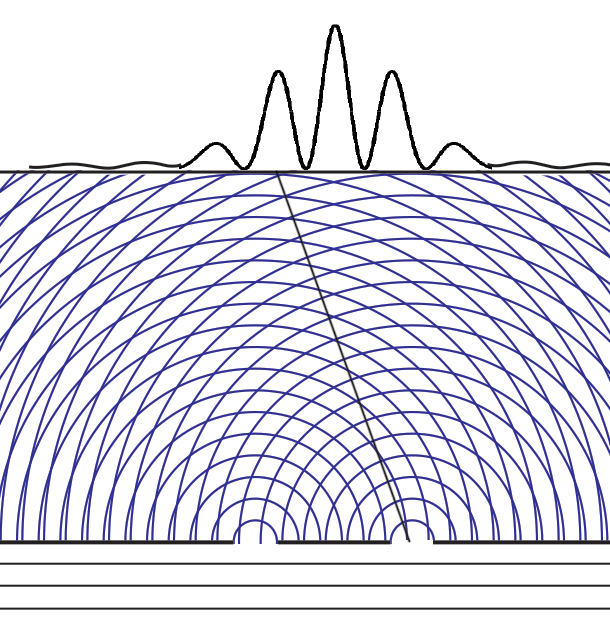The wave function depends on which slits are open, not on whether there is a particle in the experiment. ## Collapse of the Wave Function But how do we interpret the notion of the ["collapse" of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/)? At the moments just before a particle is detected at the CCD or photographic plate, there is a finite non-zero probability that the photon could be detected anywhere that the modulus (complex conjugate squared) of the probability amplitude wave function has a non-zero value. 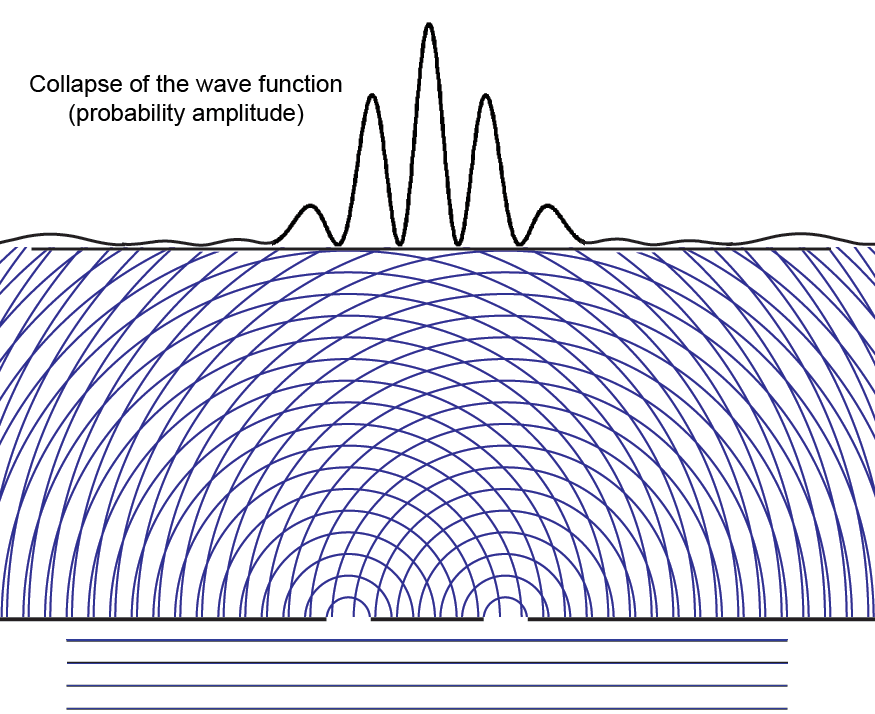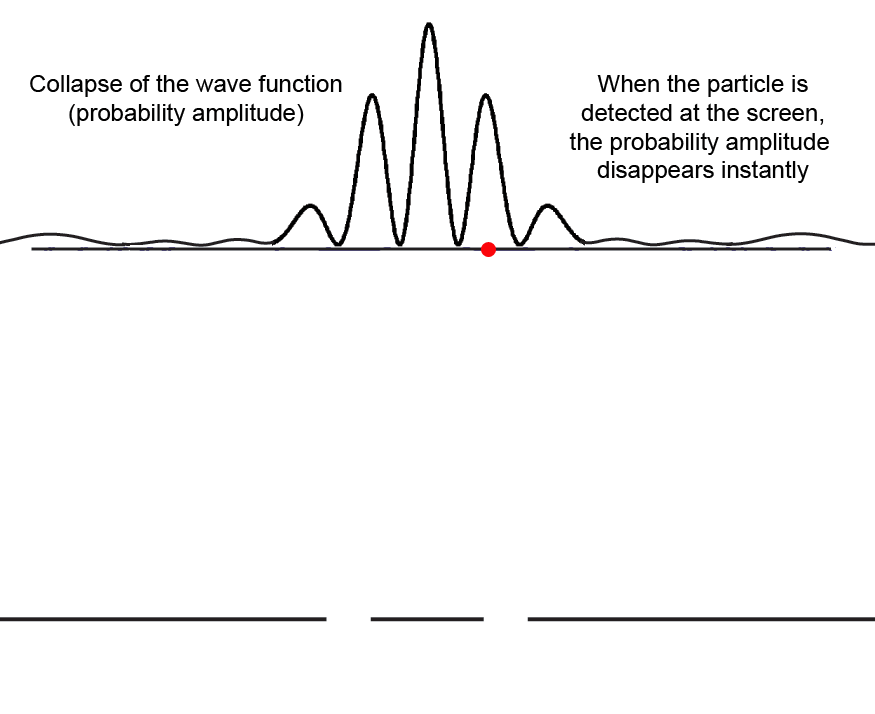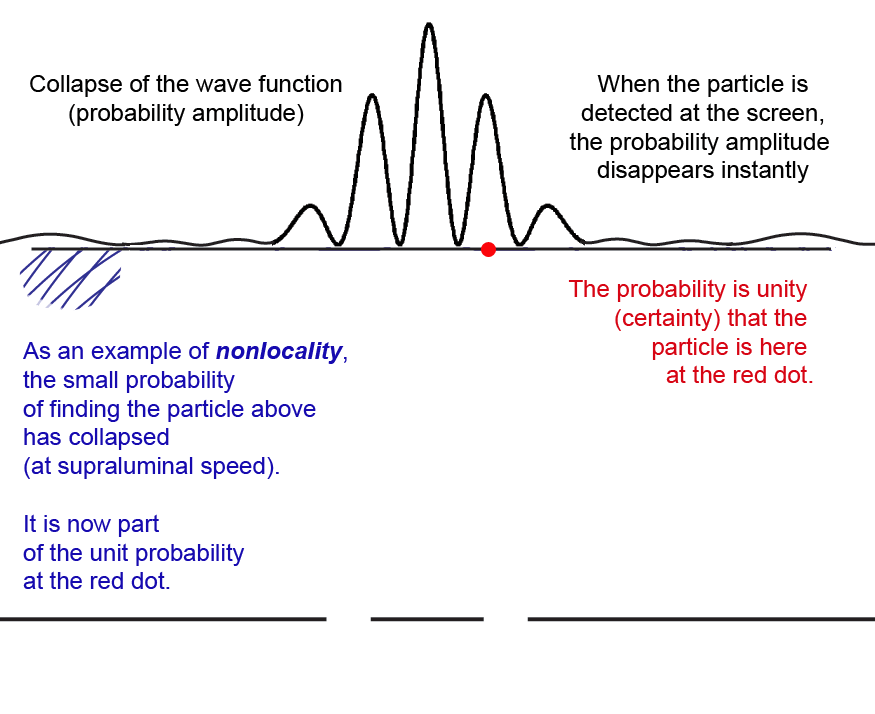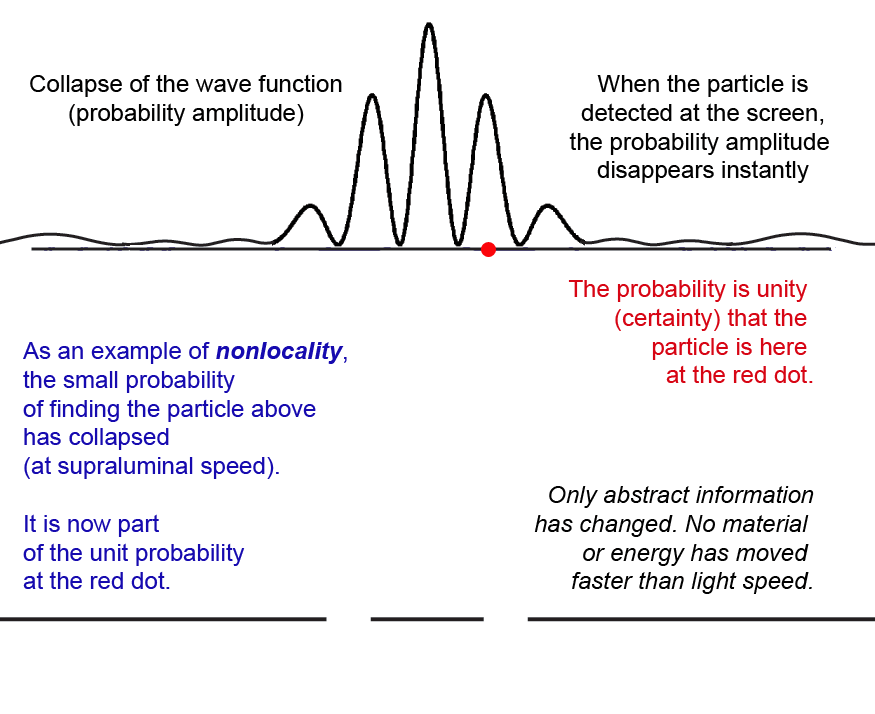If our experiment were physically very large (and it is indeed large compared to the atomic scale), we can say that the finite probability of detecting (_potentially_ measuring) the particle at position _x1_ on the screen "collapses" (goes to zero) and reappears as part of the unit probability (certainty) that the particle is at _x2_, where it is _actually_ measured. Since the collapse to zero of the probability at _x1_ is instantaneous with the measurement at _x2_, critics of quantum theory like to say that something traveled faster than the speed of light. This is most clear in the nonlocality and entanglement aspects of the [Einstein-Podolsky-Rosen](https://www.informationphilosopher.com/solutions/experiments/EPR/) experiment. But the sum of all the probabilities of measuring anywhere on the screen is not a physical quantity, it is only _immaterial information_ that "collapses" to a point. Here is what happens to the probability amplitude wave function (the blue waves) when the particle is detected at the screen (either a photographic plate or CCD) in the second interference fringe to the right (red spot). The probability simply disappears instantly. 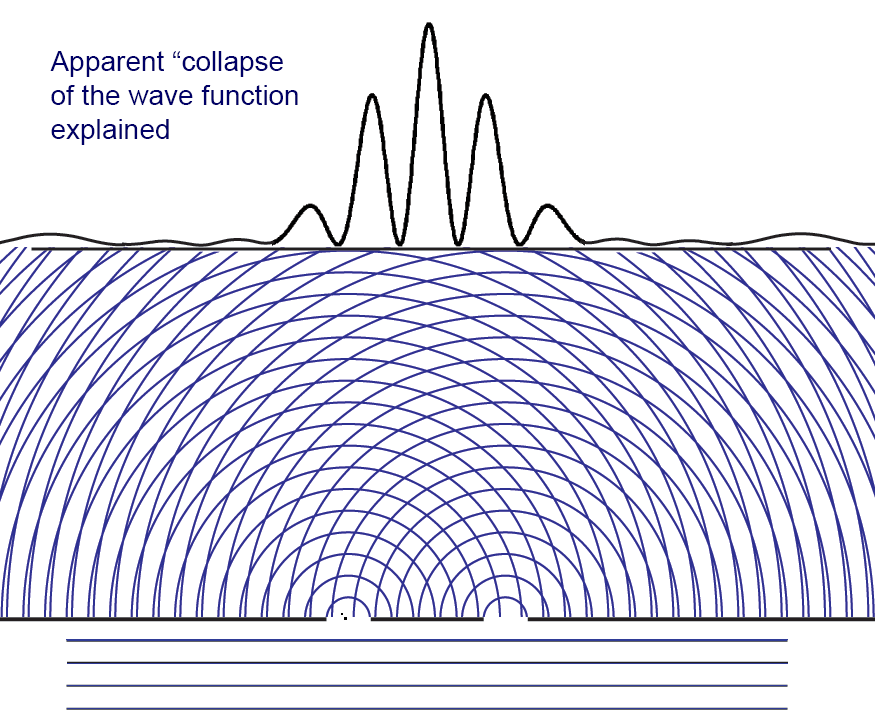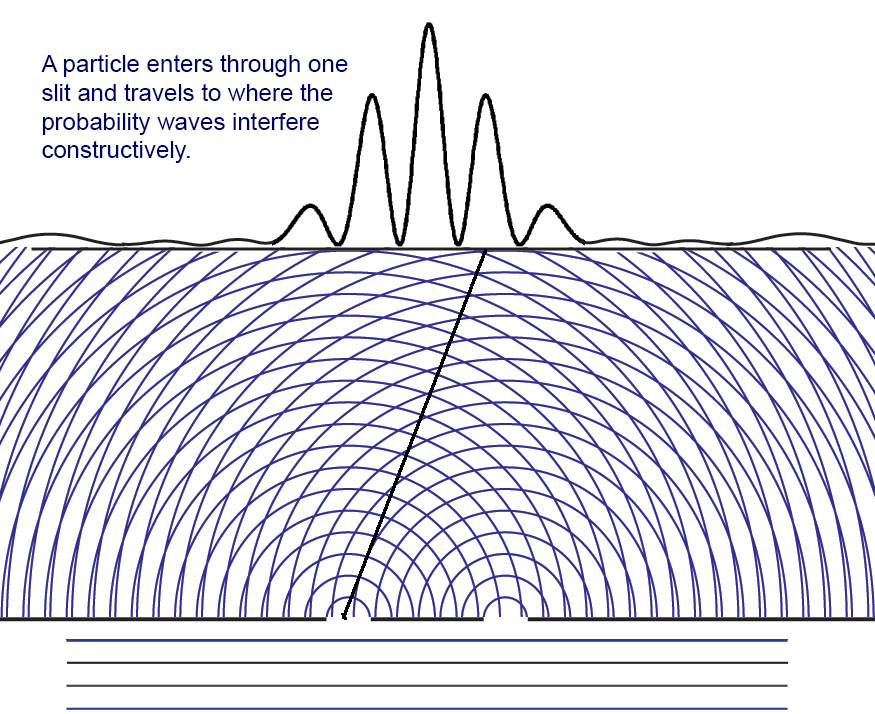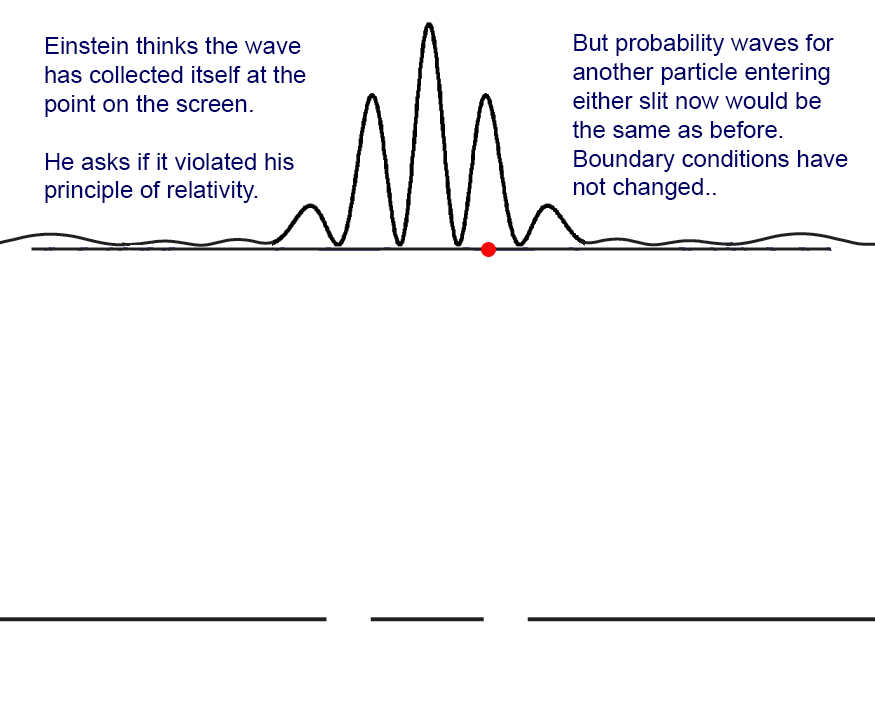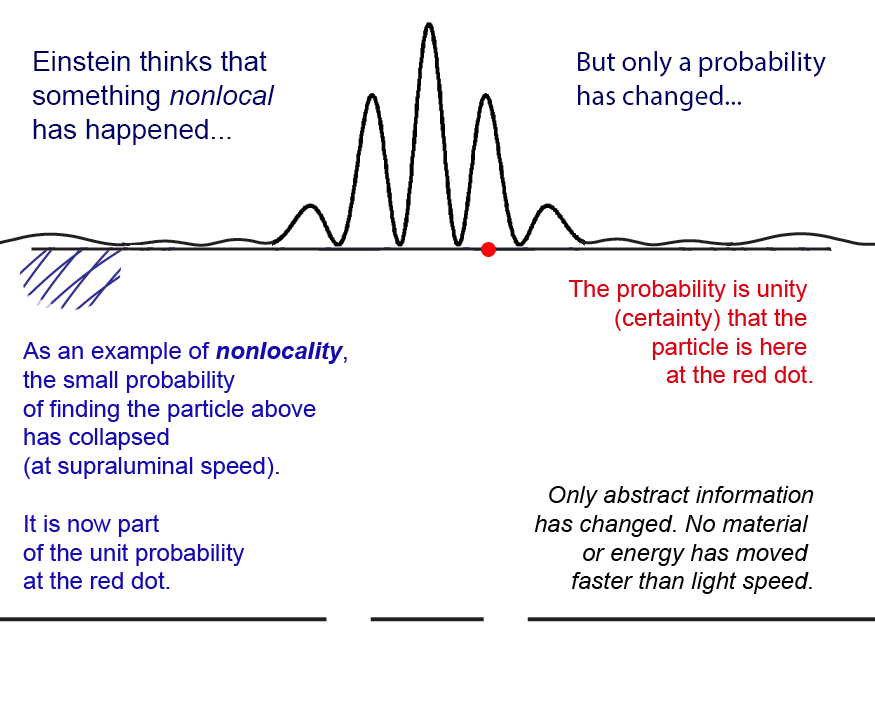## Animation of a wave function collapsing - [click to restart](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/)  Here is another version of this animation  ## History The first suggestion of two possible directions through a slit, one of which disappears ("collapses?") when the other is realized (implying a mysterious "nonlocal" correlation between the directions), was made by [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) at the 1927 Solvay conference on "Electrons and Photons." [Niels Bohr](https://www.informationphilosopher.com/solutions/scientists/bohr/) remembered the occasion with a somewhat confusing description. Here is his 1949 recollection: > At the general discussion in [Como](https://www.informationphilosopher.com/solutions/scientists/bohr/quantum_postulate.html), we all missed the presence of Einstein, but soon after, in October 1927, I had the opportunity to meet him in Brussels at the Fifth Physical Conference of the Solvay Institute, which was devoted to the theme "Electrons and Photons."  > > Note that they wanted Einstein's reaction to their work, but actually took little interest in Einstein's concern about the nonlocal implications of quantum mechanics, nor did they look at his work on electrons and photons, the theme of the conference!. > > At the Solvay meetings, Einstein had from their beginning been a most prominent figure, and several of us came to the conference with great anticipations to learn his reaction to the latest stage of the development which, to our view, went far in clarifying the problems which he had himself from the outset elicited so ingeniously. During the discussions, where the whole subject was reviewed by contributions from many sides and where also the arguments mentioned in the preceding pages were again presented, Einstein expressed, however, a deep concern over the extent to which a causal account in space and time was abandoned in quantum mechanics. 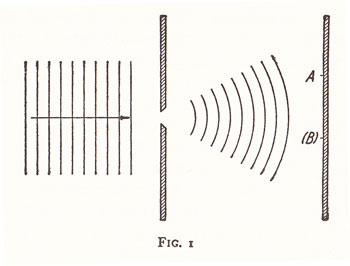> > To illustrate his attitude, Einstein referred at one of the sessions to the simple example, illustrated by Fig. 1, of a particle (electron or photon) penetrating through a hole or a narrow slit in a diaphragm placed at some distance before a photographic plate. > >  > > On account of the diffraction of the wave connected with the motion of the particle and indicated in the figure by the thin lines, it is under such conditions not possible to predict with certainty at what point the electron will arrive at the photographic plate, but only to calculate the probability that, in an experiment, the electron will be found within any given region of the plate. > > The "[nonlocal](https://www.informationphilosopher.com/problems/nonlocality/)" effects at point B are just that the _probability_ of an electron being found at point B goes to zero instantly (not an "action at a distance") when an electron is localized at point A > > The apparent difficulty, in this description, which Einstein felt so acutely, is the fact that, if in the experiment the electron is recorded at one point A of the plate, then it is out of the question of ever observing an effect of this electron at another point (B), although the laws of ordinary wave propagation offer no room for a correlation between two such events. > > > ("DIscussion with Einstein," by Niels Bohr, _Albert Einstein, Philosopher-Scientist_, P. A. Schilpp, 1949. pp.211-213) Although Bohr seems to have missed Einstein's point completely, Werner Heisenberg at least came to explain it well. In his 1930 lectures at the University of Chicago, Heisenberg presented a critique of both particle and wave pictures, including a new example of [nonlocality](https://www.informationphilosopher.com/problems/nonlocality/) that Einstein had apparently developed since 1927. It includes Einstein's concern about "action-at-a-distance" that might violate his principle of relativity, and anticipates the [Einstein-Podolsky-Rosen paradox](https://www.informationphilosopher.com/solutions/experiments/EPR/). Heisenberg wrote: > In relation to these considerations, one other idealized experiment (due to Einstein) may be considered. We imagine a photon which is represented by a wave packet built up out of Maxwell waves. It will thus have a certain spatial extension and also a certain range of frequency. By reflection at a semi-transparent mirror, it is possible to decompose it into two parts, a reflected and a transmitted packet. There is then a definite probability for finding the photon either in one part or in the other part of the divided wave packet. After a sufficient time the two parts will be separated by any distance desired; now if an experiment yields the result that the photon is, say, in the reflected part of the packet, then the probability of finding the photon in the other part of the packet immediately becomes zero. The experiment at the position of the reflected packet thus exerts a kind of action (reduction of the wave packet) at the distant point occupied by the transmitted packet, and one sees that this action is propagated with a velocity greater than that of light. However, it is also obvious that this kind of action can never be utilized for the transmission of signals so that it is not in conflict with the postulates of the theory of relativity. > > > (_The Physical Principles of the Quantum Theory_, W. Heisenberg, 1930. p.39) Clearly the "kind of action (reduction of the wave packet)" described by Heisenberg is the same "mysterious" influence that the wave function has over the places that the particle will be found statistically in a large number of experiments, including our canonical "mystery," the two-slit experiment. Apart from the statistical information in the wave function, quantum mechanics gives us only vague and uncertain information about any individual particle. This is the true source of Heisenberg's [uncertainty principle](https://www.informationphilosopher.com/freedom/uncertainty.html). It is the reason that Einstein correctly describes quantum mechanics as "incomplete." Quantum mechanics does not prove that the particle actually has no position at each instant and a path that conserves its momentum, spin, and other conserved properties. In Einstein's view of "objective reality," the particle has those properties, even if quantum mechanics prevents us from knowing them - without a measurement that destroys their interference capabilities or "decoheres" them. Some Other Animations of the Two-Slit Experiment None of these animations, viewed many millions of times, can explain why a particle entering one slit when both are open exhibits the properties of waves characteristic of two open slits. It remains Feynman's "one mystery" of quantum mechanics. PBS Digital Studios Veritasium Veritasium Wave-Particle Duality Animation One good thing in this animation is that it initially shows only particles firing at the slits. This is important historically because Isaac Newton thought that light was a stream of particles traveling along a light ray. He solved many problems in optics by tracing light rays through lenses. But without a clear verbal explanation it is hard to follow. The Fresnel-Arago Version of the Two-slit Experiment We look at the [Hamamatsu Photonics version of the Fresnel-Arago two-slit experiment](https://photonterrace.net/en/photon/single_photon/). This experiment puts polarizers at +45 and -45 degrees over the left and right slits. Let's see how the wave function explains the different results with a third polarizer (analyzer) intermediate between the slits and the screen in vertical or horizontal orientation. As [Paul Dirac explains](https://informationphilosopher.com/solutions/experiments/dirac_3-polarizers/), a 45 degree polarizer produces photons in a linear combination (or superposition) of vertical |v> and horizontal [h> states.  | d > = ( 1/√2) | v > + ( 1/√2) | h > So the photons passing through either the left or right slit are 50% vertical and 50% horizontal. But note that the vertical photons going through both slits are in phase (pointing up), while the horizontal photons going through the right slit (+45 pointing right |→>) are out of phase with those going through the left slit (-45 pointing left |←>). So when the intermediate polarizer (analyzer) is vertical, it passes photons that are in phase | ↑> |↑> and they constructively interfere, as the Hamamatsu diagrams explain. Horizontally polarized photons are absorbed. The central fringe is bright.  When the intermediate polarizer is horizontal, vertically polarized photons are absorbed, left and right photons passing straight through the slits are out of phase, |←> and |→>, and so destructively interfere, |←> |→>. The central fringe is now dark. When the angle of photons going through the slits is to the left or right, the path of light for one slit is longer, and the phase difference goes to zero at the bright fringes on either side of the dark center.  The waves (or wave functions) tell us about the probabilities of finding photons, and the angles at which they leave the slits determine their relative phases.