# Common Cause We explore the idea that simultaneous measurement outcomes at two entangled particles widely separated in space can be _correlated_ as the result of causes or conditions in the past light cone of the events, for example, symmetries and conservation laws at their entanglement state preparation. This idea opposes the standard view, developed over five decades by [Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/), that some kind of faster-than-light _instantaneous_ interaction between a particle and its wave function, or between two particles, is needed to explain [nonlocality](https://www.informationphilosopher.com/problems/nonlocality/) and [entanglement](https://www.informationphilosopher.com/problems/entanglement/). In his later years, Einstein famously called two-particle entanglement "spooky action at a distance" (_spukhafte Fernwirkung_) in a March 3, 1947 letter to [Max Born](https://www.informationphilosopher.com/solutions/scientists/born/). We shall critically examine the details of entanglement state preparations and the experimental data from particle measurements in _six different kinds of entanglement experiments_. The first three (from the 1930's to 1960's) were thought ("_gedanken_") experiments (really hypothetical theories) involving material particles, atoms and electrons. The first was Einstein's theoretical work starting in 1905 and culminating in the 1935 EPR paper, his most cited work and the touchstone for all subsequent research on entanglement. [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/)'s proposal in the 1950's that _local hidden variables_ could explain entanglement is the second kind of thought experiment. The third is the great work of [John Stewart Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) in the 1960's, including his [Bell Theorem](https://www.informationphilosopher.com/quantum/bell_theorem/) and his claim that if hidden variables exist they must be _non-local_. The fourth and the sixth kind of experiments were _actual physical_ experiments done in laboratories with entangled light particles (photons). In the 1970's John Clauser and Stuart Freedman, and in the 1980's Alain Aspect used _atomic cascades_ in calcium atoms to entangle photons. In the 1990's Anton Zeilinger and his colleagues in Vienna developed the _spontaneous parametric down conversion(SPDC)_ techniques to generate entangled photons now used in most entanglement experiments. Clauser, Aspect, and Zeilinger received the 2022 Nobel Prize in Physics for their work. Our fifth kind of entanglement study was the very popular thought experiment of [David Mermin](https://www.informationphilosopher.com/solutions/scientists/mermin/) in the 1980's. Although our focus is on experiments and their data correlations, we will also describe the mathematical quantum theory, the wave functions, [superpositions](https://www.informationphilosopher.com/quantum/superposition/) or _linear combinations_ of product states that perfectly predict the puzzling correlations. We will also indicate the initial symmetry, physical condition, or conservation laws in the entangled state preparations that may be a "common cause" for the subsequent measurements of correlated events. We cannot provide any physical mechanism or interactions between two particles that maintains the total angular momentum from moment to moment as they travel from state preparation to distant measurements, just as quantum mechanics cannot observe and describe the motions and interactions of electrons in and between different shells or orbitals in atoms and molecules. But we might say that the property of total electron spin zero is "local" in the sense that it is traveling along with each particle just as [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/)'s "hidden variables" or [David Mermin](https://www.informationphilosopher.com/solutions/scientists/mermin/)'s "instruction sets" were thought to do. And we can criticize the claim that the three components of spin angular momentum must exist and be defined in all spatial directions, x, y, and z (which is impossible), in order for experiments to find the spins opposite in all directions when measured. Finally, we will trace the history in quantum mechanics of the most powerful common cause of all, the idea that every physical event can be traced back to a chain of causes and effects that goes back to the [creation of the universe](https://www.informationphilosopher.com/introduction/creation/). ## 1) Einstein and the [EPR paradox](https://www.informationphilosopher.com/solutions/experiments/EPR/). Einstein first described _two particles_ exhibiting [nonlocal](https://www.informationphilosopher.com/problems/nonlocality/) behavior in a conversation with Leon Rosenfeld at a meeting in Berlin in 1933. Before this, nonlocality was between a single light quantum and its light wave. In 1933, shortly before he left Germany to emigrate to America, Einstein attended a lecture on quantum electrodynamics by Léon Rosenfeld. Keep in mind that Rosenfeld was perhaps the most dogged defender of the Copenhagen Interpretation. After the talk, Einstein asked Rosenfeld, > “What do you think of this situation?” Suppose two particles are set in motion towards each other with the same, very large, momentum, and they interact with each other for a very short time when they pass at known positions. Consider now an observer who gets hold of one of the particles, far away from the region of interaction, and measures its momentum: then, from the conditions of the experiment, he will obviously be able to deduce the momentum of the other particle. If, however, he chooses to measure the position of the first particle, he will be able tell where the other particle is. > (_Niels Bohr, His Life and Work as seen by His Friends and Colleagues_, 1967, S. Rozental, pp.128-129) It is most unfortunate that Einstein did not explain that measuring the momentum of the first particle allows us to deduce the momentum of the second particle because of the _conservation of linear momentum_. The same conservation principle explains, as Einstein says, "If, however, he chooses to measure the position of the first particle, he will be able to tell where the other particle is." If Einstein had called this ability "_knowledge (information) at a distance_," instead of "spooky _action_ at a distance," entanglement might never have been thought "spooky". It would be just a correlation of physical properties resulting from a common cause and a conservation law. Einstein and colleagues [Boris Podolsky](http://en.wikipedia.org/wiki/Boris_Podolsky) and [Nathan Rosen](http://en.wikipedia.org/wiki/Nathan_Rosen), proposed in 1935 a paradox (known by their initials as [EPR](https://www.informationphilosopher.com/solutions/experiments/EPR/) or as the [Einstein-Podolsy-Rosen paradox](https://www.informationphilosopher.com/solutions/experiments/EPR/)) to exhibit internal contradictions in the new quantum physics. They hoped to show that quantum theory could not describe certain intuitive "elements of reality" and thus was incomplete. They said that, as far as it goes, quantum mechanics is _correct_, just not "complete." Einstein was correct that quantum theory is "_incomplete_" relative to classical physics, which has twice as many dynamical variables that can be known with arbitrary precision. But half of this information is missing in quantum physics, due to the [indeterminacy principle](https://www.informationphilosopher.com/freedom/indeterminacy.html) which allows only one of each pair of non-commuting observables (for example momentum _or_ position) to be known with arbitrary accuracy. Even more important, an individual particle, _cannot be said to have a known position before a measurement_, since evolution described by the unitary and [deterministic](https://www.informationphilosopher.com/freedom/determinism.html) Schrödinger equation provides us only [probabilities](https://www.informationphilosopher.com/freedom/probability.html). The most that can be said is that the particle can be found anywhere the probability amplitude is non-zero. This was the core idea of Einstein's claim of "incompleteness." For Bohr to deny this and call quantum mechanics "complete" was just to play word games, which infuriated Einstein. Einstein was also correct that indeterminacy makes quantum theory an irreducibly _discontinuous_ and _statistical_ theory. Its predictions and highly accurate experimental results are statistical in that they depend on an _ensemble_ of identical experiments, not on any individual experiment. Einstein wanted physics to be a continuous field theory, in which all physical variables are completely and locally determined by the four-dimensional field of space-time in his theory of relativity. Einstein and his colleagues [Erwin Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/), [Max Planck](https://www.informationphilosopher.com/solutions/scientists/planck/), (later [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/)), and others hoped for a return to deterministic physics, and the elimination of mysterious quantum phenomena like the [_superposition of states_](https://www.informationphilosopher.com/solutions/experiments/dirac_three-polarizers/), the mysterious ["collapse" of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/), and [Schrödinger's famous cat](https://www.informationphilosopher.com/solutions/experiments/schrodingerscat/). EPR continues to fascinate [determinist](https://www.informationphilosopher.com/freedom/determinism.html) philosophers of science who hope to prove that [quantum indeterminacy](https://www.informationphilosopher.com/freedom/indeterminacy.html) does not exist. What happens according to the [information interpretation of quantum mechanics](https://www.informationphilosopher.com/introduction/physics/interpretation/) is an instantaneous change in the [information](https://www.informationphilosopher.com/introduction/information/) about [probabilities](https://www.informationphilosopher.com/freedom/probability.html) (actually complex probability amplitudes). Nothing physical (matter or energy) is moving anywhere. As we've seen, Einstein had been bothered by "nonlocal" phenomena between a light quantum and its light wave (function) since his 1905 photoelectric paper. But this phenomenon was even more clearly exhibited in EPR experiments as the _apparent_ transfer of something physical, an "action," from one particle to another particle faster than the speed of light. The 1935 paper was based on Einstein's 1933 question to Leon Rosenfeld about two material particles fired in opposite directions from a central source with equal velocities. He imagined them starting at _t0_ some distance apart and approaching one another with high velocities. Then for a short time interval from _t1_ to _t1 + Δt_ the particles are in contact with one another. After the particles are measured and become entangled at _t1_, quantum mechanics describes them with a single two-particle wave function Ψ12 that is not the simple product of two one-particle wave functions Ψ1 and Ψ2. Einstein said that at a later time _t2_, a measurement of one particle's position would instantly establish the position of the other particle - _without measuring it explicitly_. And this is correct, just as after the collision of two billiard balls, measurement of one ball tells us exactly where the other one is due to conservation of momentum. But this is not "action at a distance." It is more nearly "knowledge at a distance." Note that Einstein is _implicitly_ using _conservation of linear momentum_ to know the position of the second particle. Although conservation laws are rarely cited as the explanation, they may be the physical reason that entangled particles _always_ produce correlated results. If the results were not always correlated, the implied violation of a fundamental conservation law would be a much bigger story than mysterious entanglement itself, as interesting as that is. This idea of something measured in one place "influencing" measurements far away challenged what Einstein thought of as "local reality." Einstein thought that when the particles moved far enough apart they could be treated as _separated_, with independent wave functions Ψ1 and Ψ2. But [Erwin Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/) quickly replied to the EPR paper, telling Einstein that his "separation principle" (_Trennungsprinzip_) was not correct. The particles can not be separated into a product of independent wave functions, for example, particle A in state 1, particle B in state 2, Ψ12 ≠ Ψ1A Ψ2B Instead, particles A and B are each _randomly_ found in state 1 or 2. But Particle B is certain to be in state 2 if particle A is measured in state 1. Ψ12 = 1/√2 (Ψ1A Ψ2B) + 1/√2 (Ψ2A Ψ1B) Quantum mechanics says that the particles are not in "pure" quantum states, but a "mixture" of two states, which maintain the coherent phase relations that allow them to interfere with one another. Schrödinger used [Paul Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/)'s 1926 [principle of superposition](https://www.informationphilosopher.com/quantum/superposition/) and [John von Neumann](https://www.informationphilosopher.com/solutions/scientists/dirac/)'s 1932 motion of "mixed states" in the "density matrix" to create two of the most popular and controversial ideas in quantum mechanics. First, Schrödinger described the two particles as "entangled" at their first encounter. He called it _verschränkt_ in German. _Verschränkt_ means something like cross-linked. It describes someone standing with arms crossed, where each arm reaches out to touch the other. Today EPR is the classic example of entanglement. Second, Schrödinger introduced his famous cat, claiming it is in a _mixed state_ or a _superposition_ of live and dead cats! It was at this point in quantum history that the most controversial two-particle equation above appeared that combines the [ontological chance](https://www.informationphilosopher.com/quantum/chance/) that Einstein discovered in 1916 with the idea that one quantum state can be described as in a _linear combination_ or _superposition_ of two other states which Dirac introduced in his transformation theory of quantum mechanics in 1927. In Dirac's theory, the squared coefficients of the two states give us the _probabilities_ of finding the particles in the one or the other state. The equation combines quantum _randomness_ with quantum _interference_. Interference was made famous in the [two-slit experiment](https://www.informationphilosopher.com/quantum/two-slit/), which Richard Feynman almost thirty years after EPR called the “one mystery,” the _only_ mystery at the heart of quantum mechanics. Note that the equation does not describe two _material_ particles _interacting_ with one another but their abstract _immaterial_ wave functions Ψ1 and Ψ2 _interfering_ with one another. These quantum mechanical wave functions, solutions to Schrödinger’s equations of motion (which replace Newton's equations of motion in classical mechanics), were thought by Schrödinger to be describing matter or energy, photons for light waves, mass and perhaps electric charge for electrons. But in the quantum mechanics of Heisenberg, Jordan, Born, and Dirac the wave functions became “probability amplitudes,” whose absolute squares predict the _probability_ of finding the values of observable quantum properties. And those predictions have been confirmed with extraordinary accuracy by countless experiments. Let’s look at the equation in its simplest form that describes the superposition state of Schrödinger’s cat. | Cat > = ( 1/√2) | Live > + ( 1/√2) | Dead > Although this equation predicts interference between the cat states, such interference is never seen in cats, though it has been measured in surprisingly large macroscopic objects. Nevertheless, squaring the coefficients 1/√2 tells us that there is 50% chance of finding such a cat in either the live or dead state, i.e., which is confirmed in principle. Cats = (1/2) Live + (1/2) Dead. Let's see how this simple equation also describes the two-slit experiment. Ψ = ( 1/√2) | Left > + ( 1/√2) | Right > The wave function past the two slits is a linear combination or _superposition_ of the wave function passing the left slit | Left > with the wave function passing the right slit | Right >. Note that whichever slit the particle passes through (and it must go through just one, because a quantum particle cannot become two, violating conservation of mass and/or energy), the probabilities of finding it on the screen are determined by the two-slit superposition. If a particle was detected passing through the left slit, or if the right slit were closed, the interference pattern would depend only on that slit's wave function | Left >. Given that the double-slit interference appears even if _only one particle at a time_ is incident on the two slits, we see why many say that the particle interferes with itself. But it is the wave function alone that is interfering with itself. Whichever slit the particle goes through, it is the probability amplitude ψ, whose squared modulus |ψ|2 gives us the probability of finding a particle somewhere, the interference pattern. It is what it is because _the two slits are open_.  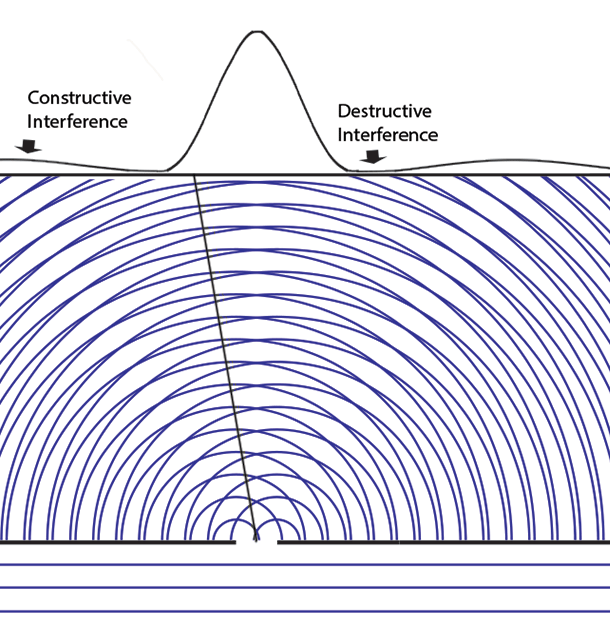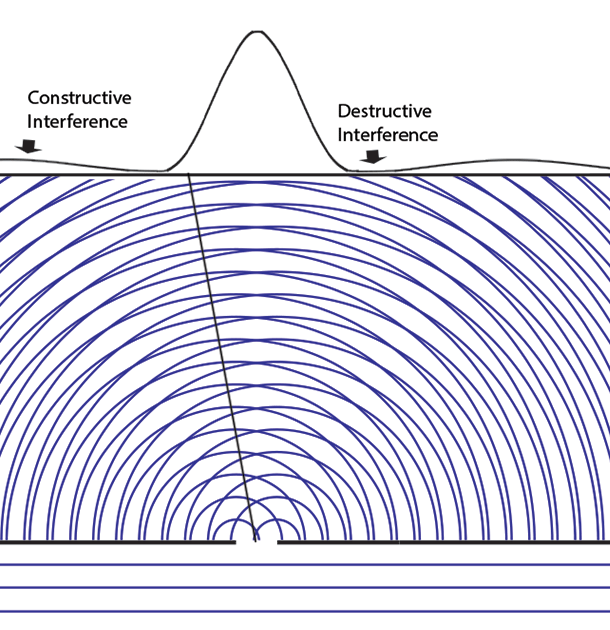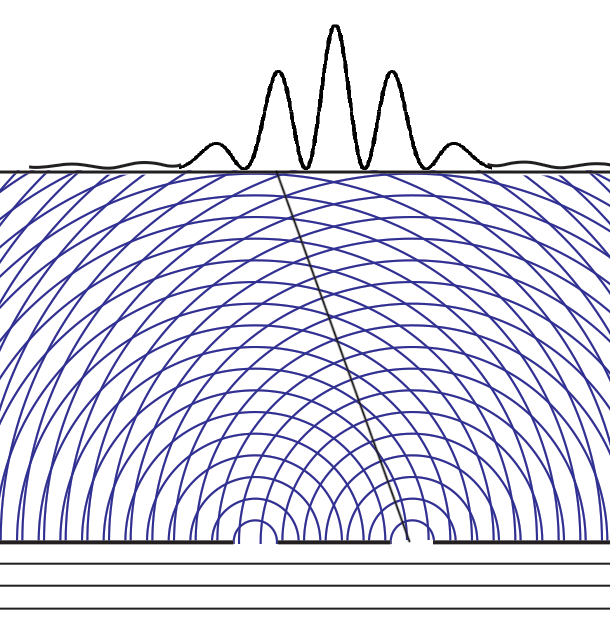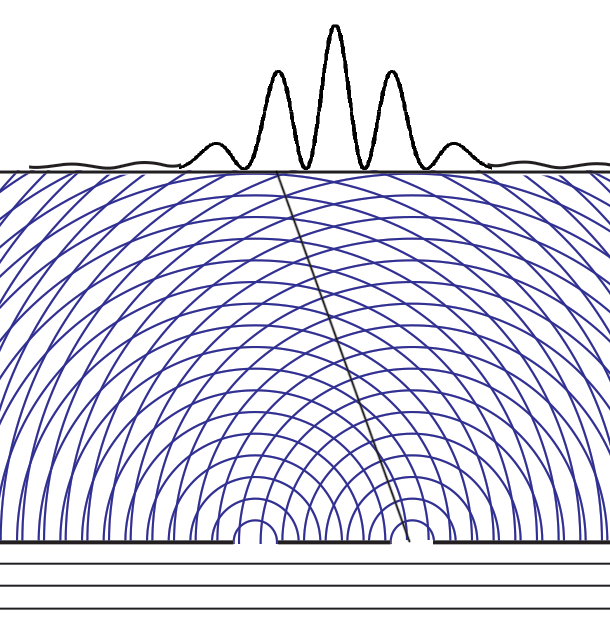This is the deepest metaphysical mystery in quantum mechanics. How can an abstract _immaterial_ probability wave _influence_ the particle paths to show interference when large numbers of independent particles are collected? 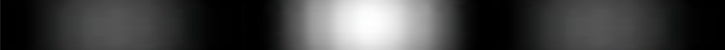**Why interference patterns show up when both slits are open, even when particles go through just one slit, though we cannot know which slit or we lose the interference** | | | |---|---| ||| || | |When there is only one slit open (here the left slit), the probabilities pattern has one large maximum (directly behind the slit) and small side fringes. If only the right slit were open, this pattern would move behind the right slit.<br><br>If we add up the results of some experiments with the left slit open and others with the right open we don't see the multiple fringes that appear with two slits open.<br><br>|When both slits are open, the maximum is now at the center between the two slits, there are more interference fringes, and these probabilities apply _whichever slit the particle enters_. The solution of the Schrödinger equation depends on the boundary conditions - different when two holes are open. The "one mystery" remains - how these "probabilities" can exercise causal control (statistically) over matter or energy particles.<br><br>Feynman's path integral formulation of quantum mechanics suggests the answer. His "virtual particles" explore all space (the "sum over paths") as they determine the variational minimum for least action, thus the resulting probability amplitude wave function can be said to "know" which holes are open.| Einstein criticized the [collapse of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) as "instantaneous-action-at-a-distance." This criticism resembles the criticisms of Newton's theory of gravitation. Newton's opponents charged that his theory was "action at a distance" and instantaneous. Einstein's own field theory of general relativity shows that gravitational influences travel at the speed of light and are mediated by a gravitational field that shows up as curved space-time. For Einstein, fields like gravitation and electromagnetism are "_ponderable_." A disturbance of the field at one place is propagated at some finite velocity to other parts of the field. But mathematical probability is not a ponderable field in this sense. When a probability function collapses to unity in one place and zero elsewhere, nothing physical, neither matter nor energy, is moving from one place to the other. Only information changes. For a detailed history of Einstein's concerns about single-particle nonlocality over the thirty years before EPR, see [this page](https://www.informationphilosopher.com/solutions/scientists/einstein/#light-quantum). ## 2) David Bohm and hidden variables. In our second kind of "thought experiment," [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/) replaced Einstein's separating particles with a hydrogen molecule disassociating into two hydrogen atoms, each with ℏ/2 of spin angular momentum. Instead of measuring linear momentum, Bohm proposed using two hydrogen atoms that are prepared in an initial state of known total spin angular momentum zero (the H2 molecule). Momentum and position are _continuous_ variables. Spin is _discrete_. Bohm argued that measurements of discrete variables would be more precise. Bohm also proposed _local_ "hidden variables" might be needed to explain the correlations. Here is his description. Note that it includes the two-particle wave function describing the superposition of mixed states. > We consider a molecule of total spin zero consisting of two atoms, each of spin one-half. The wave function of the system is therefore > > _ψ_ = (1/√2) [ _ψ+ (1) ψ- (2) - ψ- (1) ψ+ (2)_ ] > > where ψ_+_ (1) refers to the wave function of the atomic state in which one particle (A) has spin +ℏ/2, etc. The two atoms are then separated by a method that does not influence the total spin. After they have separated enough so that they cease to interact, any desired component of the spin of the first particle (A) is measured. Then, because the total spin is still zero, it can immediately be concluded that the same component of the spin of the other particle (B) is opposite to that of A. > > > "Discussion of Experimental Proof for the Paradox of Einstein, Rosen, and Podolsky,” _Physical Review_, vol.108, no.4. p.1070, 1957 Note that when Bohm says "_because the total spin is still zero, it can immediately be concluded that the same component of the spin of the other particle (B) is opposite to that of A,_" he is _implicitly_ using the conservation of total spin angular momentum. Note also that our superposition equation for the two particles predicts a 50% chance that the first particle will be spin up (_ψ+_ (1)) and the second down (_ψ-_ (2)) and a 50% chance of the reverse, that the first particle will be spin down (_ψ-_ (1)) and the second will be up (_ψ+_ (2)). In either case the total spin is always _certain_ to be conserved as zero. Next note that while the total spin is _certain_ to be zero, the outcome for each particle is completely _random_, half the outcomes are found up and the other half outcomes down. Finally note that these amazing predictions of outcomes _individually random_ but together _perfectly correlated_, as confirmed by numerous experiments, provide us with no _mechanisms_, no _interactions_ between the particles that produce these perfectly correlated outcomes. It is simply that as Bohm says, "because the total spin is still zero, it can immediately be concluded that the same component of the spin of the other particle (B) is opposite to that of A." We can ask ourselves whether our first thought experiment (EPR) really needed some mechanism, some interaction, as Einstein feared, to keep the particles moving symmetrically away from their center? In the absence of an external asymmetric force, their motions are mirror images, preserving their original symmetry and their conservation of total linear momentum. If linear momentum can be conserved (by symmetry) without instantaneous interactions, isn't conservation of spin angular momentum a much more plausible explanation than impossible faster-than-light interactions? In 1964, [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) made a study of EPR and David Bohm's suggestion of local hidden variables that could provide a mechanism to explain entanglement. Bell proposed an experiment using photons and polarizers that measures the angular dependence of the falloff in perfect correlations when experimenters at A and B (usually called Alice and Bob) don't set their polarizers at the same angle (which we argue is needed to preserve the symmetry of the initial entanglement and the conservation of critical properties like spin angular momentum). Correlations are perfect when they measure at the same (pre-agreed-upon) angle. When their polarizer angles differ by ninety degrees, all correlations are lost. At intermediate angle differences θ, correlations diminish proportional to the square of the cosine of their angle difference - cos2θ. ## 3) John Bell and His Inequalities. ## 4) John Clauser, Stuart Freedman, Alain Aspect, and the atomic cascade. ## 5) David Mermin and Instruction Sets. ## 4) Anton Zeilinger and spontaneous parametric down conversion (SPDC).