# Bell's Theorem [John Bell](https://www.informationphilosopher.com/solutions/scientists/bell/) showed in 1964 how the 1935 "thought experiment" of [Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/), Podolsky, and Rosen ([EPR](https://www.informationphilosopher.com/solutions/experiments/EPR/)) could be made into a real experiment. Einstein was especially bothered by the "nonlocal" aspect of quantum mechanics exhibited by a [measurement](https://www.informationphilosopher.com/problems/measurement/) at one place instantaneously determining the properties (position and momentum, and later spin) of a particle detected at another place. The spacelike separation between the two measurements implied something "travelling" faster than the speed of light between the two. Actually, at the 1927 Solvay Conference, Einstein had already complained about "action at a distance" and faster-than-light effects when, in a single-slit version of the [two-slit experiment](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/), the detection of a single particle at one place instantaneously [collapsed the probability (Ψ2)](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/) of finding it at a distant place. And we now know that Einstein probably saw this implicit violation of his theory of special relativity as early as 1905, when he formulated both relativity theory and the light-quantum hypothesis. See our [history of Einstein's thought](https://www.informationphilosopher.com/solutions/scientists/einstein/). EPR proposed the existence of supplementary parameters or "local hidden variables" that could communicate information between the two measurements. Einstein's colleagues [Erwin Schrödinger](https://www.informationphilosopher.com/solutions/scientists/schrodinger/), [Max Planck](https://www.informationphilosopher.com/solutions/scientists/planck/), [David Bohm](https://www.informationphilosopher.com/solutions/scientists/bohm/), and others hoped that the hidden variables would allow a return to deterministic physics. They wanted to eliminate [mysterious](https://www.informationphilosopher.com/freedom/mysteries.html) quantum phenomena like _superposition of states_, quantum entanglement and nonlocality, action at a distance, and - perhaps most important for Schrödinger - the irreducible statistical [chance](https://www.informationphilosopher.com/freedom/chance.html) associated with the [collapse of the wave function](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/). Einstein's famous remark on [quantum indeterminacy](https://www.informationphilosopher.com/freedom/indeterminacy.html) was that "God does not play dice." According to Wolfgang Pauli (in correspondence with [Max Born](https://www.informationphilosopher.com/solutions/scientists/born/)), Einstein was less concerned with the return of determinism than he was with the restoration of "local reality" and the elimination of "action at a distance." In 1964, John Bell put limits on any supplementary parameters or "hidden variables" that might eliminate nonlocality and restore a deterministic physics in the form of what he called an "inequality," the violation of which would confirm standard quantum mechanics. Bell also described his key assertions in the simple idea that _"local hidden variables" will never be found that give the same results as quantum mechanics_. This has come to be known as [Bell's Theorem](https://www.informationphilosopher.com/solutions/experiments/bells_theorem/). In a 1990 lecture at CERN, shortly before his untimely death, Bell made it plain that the violation of his inequality had shown the "Einstein program" to be a failure. > It just is a fact that quantum mechanical predictions and experiments, in so far as they have been done, do not agree with [my] inequality. And that's just a brutal fact of nature... No action at a distance led you to determinism, in the case of parallel polarisers, but determinism, in the case of off-parallel polarisers, leads you back to action at a distance. Now, in my opinion, in answer to the question that you posed at the beginning, I don't know this phrase is too strong and active an assertion, I cannot say that action at a distance is required in physics. But I can say that you cannot get away with no action at a distance. You cannot separate off what happens in one place and what happens in another. Somehow they have to be described and explained jointly. Well, that's just the fact of the situation; the Einstein program fails, that's too bad for Einstein, but should we worry about that? > > [**See a 10-minute video of John Bell on the Einstein failure**](https://www.informationphilosopher.com/solutions/scientists/bell/inequality_video/) Bell's Theorem has been tested in numerous real [EPR](https://www.informationphilosopher.com/solutions/experiments/EPR/) experiments over the years, by John Clauser, Alain Aspect, Michael Horne, Albert Shimony, and Richard Holt (in various [CHSH-type](http://en.wikipedia.org/wiki/CHSH_Bell_test) experiments) and most recently by [Nicolas Gisin](https://www.informationphilosopher.com/solutions/scientists/gisin/) and his colleagues in Geneva with entangled photons sent over miles of fiber optics. In the 1989 book, _Sixty-two Years of Uncertainty_, Abner Shimony summarized the significance of various versions of Bell's Theorem. > All versions of Bell's theorem are variations, and usually generalizations, of the pioneering paper of J.S. Bell of 1964, entitled "On the [Einstein-Podolsky-Rosen Paradox](https://www.informationphilosopher.com/solutions/experiments/EPR/)." All of them consider an ensemble of pairs of particles prepared in a uniform manner, so that statistical correlations may be expected between outcomes of tests performed on the particles of each pair. If each pair in the ensemble is characterized by the same quantum state Φ, then the quantum mechanical predictions for correlations of the outcomes can in principle be calculated when the tests are specified. On the other hand, if it is assumed that the statistical behavior of the pairs is governed by a theory which satisfies certain independence conditions (always similar to the Parameter and Outcome Independence conditions stated below, though the exact details vary from version to version of Bell's theorem), then it is possible to derive a restriction upon the statistical correlations of the outcomes of tests upon the two particles. The restriction is stated in the form of an inequality, known by the collective name of "Bell's Inequality." Each version of Bell's theorem exhibits a choice of Φ and of the tests upon the two particles such that the quantum mechanical predictions of correlations violates one of the Bell's Inequalities. The theorem therefore asserts that no physical theory satisfying the specified independence conditions can agree in all circumstances with the predictions of quantum mechanics. The theorem becomes physically significant when the experimental arrangement is such that relativistic locality prima facie requires that the independence conditions be satisfied. Because such arrangements are in principle possible (and, in fact, actually realizable, if certain reasonable assumptions are made), one can restate Bell's Theorem more dramatically as follows: no local physical theory can agree in all circumstances with the predictions of quantum mechanics. > > 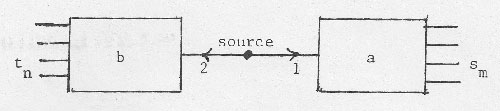 Fig. 1. An ensemble of particle pairs 1 + 2 is emitted in a uniform manner from the source. Particle 1 enters an analyzer with a controllable parameter a, and the possible outcomes are sm (m = 1,2,...). Particle 2 enters an analyzer with controllable parameter b, and the possible outcomes are tn (n = 1,2,...). > > Figure 1 shows a source from which particle pairs, labeled 1 and 2, are emitted in a uniform manner. The complete state of a pair 1+2 is denoted by k, where k belongs to a space K of complete states. No assumption is made about the structure of K, except that probability measures can be defined on it. Because of the uniform experimental control of emission, it is reasonable to suppose that there is a definite probability measure w defined over K which governs the ensemble of pairs; but the uniformity need not be such that w is a delta-function, i.e., that every pair of the ensemble is in the same complete state k. Particle 1 enters an analyzer with a controllable parameter a, which the experimenter can specify, for instance, by turning a knob. Likewise, particle 2 enters an analyzer with a controllable parameter b. > > (Abner Shimony, "An Exposition of Bell's Theorem," in _Sixty-two Years of Uncertainty_, pp.33-34) The reason philosophers like Shimony have difficulty with two-particle wave-function collapses is clear from his exposition. It is quite wrong to describe two distinct particles, 1 and 2, with 1 entering the right analyzer and 2 entering the left analyzer. Just as a single particle cannot be localized in the [two-slit experiment](https://www.informationphilosopher.com/solutions/experiments/two-slit_experiment/), neither particle in an EPR experiment is localizable until there is a [measurement](https://www.informationphilosopher.com/problems/measurement/), at which time both become localized (to within the usual [quantum indeterminacy)](https://www.informationphilosopher.com/freedom/indeterminacy.html) however far apart they are at that time (in the rest frame of the experiment). The reason we know everything about the "other" particle as soon as we measure one is, as Einstein knew well, but later writers often ignore, found in the various conservation laws (of energy, momentum, spin, etc.). If Bell's inequalities were not violated, the much more fundamental laws of conservation of momentum, angular momentum and spin would be violated. For a correct description of how quantum mechanics describes two particles in an entangled quantum state, see [our description of the EPR experiment](https://www.informationphilosopher.com/solutions/experiments/EPR/#visualization).