# Dirac's Principles of Quantum Mechanics
In his great textbook _The Principles of Quantum Mechanics_, [P. A. M. (Paul) Dirac](https://www.informationphilosopher.com/solutions/scientists/dirac/) gave us his three basic concepts from which all of non-relativistic quantum mechanics follows.
He actually gave us just one [principle](https://www.informationphilosopher.com/quantum/principles/#principle), one [axiom](https://www.informationphilosopher.com/quantum/principles/#axiom), and one [postulate](https://www.informationphilosopher.com/quantum/principles/#postulate).
1. _The Principle of Superposition_.
The Schrōdinger equation (1) is a _linear_ equation. It has no quadratic or higher power terms, and this introduces a profound - and for many scientists and philosophers a disturbing - feature of quantum mechanics, one that is _impossible in classical physics_, namely the principle of superposition of quantum states. If _ψa_ and _ψb_ are both solutions of equation (1), then an arbitrary linear combination of these,
| _ψ_ > = ca | _ψa_ > + cb | _ψb_ >, (4)
with complex coefficients ca and cb, is also a solution.
Together with Born's probabilistic (statistical) interpretation of the wave function, the principle of superposition accounts for the major mysteries of quantum theory, some of which we hope to resolve, or at least reduce, with an objective (observer-independent) explanation of _irreversible_ [information creation](https://www.informationphilosopher.com/quantum/principles/introduction/creation/) during quantum processes.
Observable information is critically necessary for measurements, though observers can come along anytime after the information comes into existence as a consequence of the interaction of a quantum system and a measuring apparatus.
The quantum (discrete) nature of physical systems results from there generally being a large number of solutions _ψn_ (called eigenfunctions) of equation (1) in its time independent form, with energy eigenvalues _En_.
_H ψn_ = _En ψn_, (5)
The discrete spectrum energy eigenvalues _En_ limit interactions (for example, with photons) to specifi�c energy diff�erences _En_ - _Em_.
In the old quantum theory, Bohr postulated that electrons in atoms would be in "stationary states" of energy _En_, and that energy differences would be of the form _En_ - _Em_ = _hν_, where _ν_ is the frequency of the observed spectral line.
Einstein, in 1916, _derived_ these two Bohr postulates from basic physical principles in his paper on the emission and absorption processes of atoms. What for Bohr were assumptions, Einstein grounded in quantum physics, though virtually no one appreciated his foundational work at the time, and few appreciate it today, his work eclipsed by the Copenhagen physicists.
The eigenfunctions _ψn_ are orthogonal to each other
< _ψn | ψm_ > = δnm (6)
where the "delta function"
δnm = 1, if _n = m_, and = 0, if _n ≠ m_. (7)
Once they are normalized, the _ψn_ form an orthonormal set of functions (or vectors) which can serve as a basis for the expansion of an arbitrary wave function _φ_ �
| _φ_ > = ∑ n = 0 n = ∞ _cn_ | _ψn_ >. (8)
The expansion coefficients are
_cn_ = < _ψn_ | _φ_ >. (9)
In the abstract Hilbert space, < _ψn_ | _φ_ > is the "projection" of the vector _φ_ onto the orthogonal axes _ψn_ of the _ψn_ "basis" vector set.
1.1 An example of superposition.
Dirac tells us that a diagonally polarized photon can be represented as a _superposition_ of vertical and horizontal states, with complex number coefficients that represent "_probability amplitudes_." Horizontal and vertical polarization eigenstates are the only "_possibilities_," if the measurement apparatus is designed to measure for horizontal or vertical polarization.
Thus,
| _d_ > = ( 1/√2) | _v_ > + ( 1/√2) | _h_ > (10)
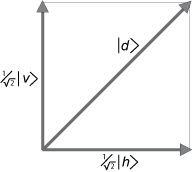
The vectors (wave functions) _v_ and _h_ are the appropriate choice of basis vectors, the vector lengths are normalized to unity, and the sum of the squares of the probability amplitudes is also unity. This is the orthonormality condition needed to interpret the (squares of the) wave functions as _probabilities_.
When these (in general complex) number coefficients (1/√2) are squared (actually when they are multiplied by their complex conjugates to produce positive real numbers), the numbers (1/2) represent the probabilities of finding the photon in one or the other state, should a measurement be made on an initial state that is diagonally polarized.
Note that if the initial state of the photon had been vertical, its projection along the vertical basis vector would be unity, its projection along the horizontal vector would be zero. Our probability predictions then would be - vertical = 1 (certainty), and horizontal = 0 (also certainty). Quantum physics is not always [uncertain](https://www.informationphilosopher.com/freedom/uncertainty.html), despite its reputation.
2. _The Axiom of Measurement_.
The axiom of measurement depends on the idea of "observables," physical quantities that can be measured in experiments. A physical observable is represented as an operator _A_ that is "Hermitean" (one that is "self-adjoint" - equal to its complex conjugate, _A*� = A_). The diagonal _n, n_ elements of the operator's matrix,
< _ψn | A | ψn_ > = ∫ ∫ _ψ* (q) A (q) ψ (q) dq_, (11)
are interpreted as giving the expectation value for _An_ (when we make a measurement).
The molecule suffers a recoil in the amount of _hν/c_ during this elementary process of emission of radiation; the direction of the recoil is, at the present state of theory, determined by "chance"...
The weakness of the theory is, on the one hand, that it does not bring us closer to a link-up with the wave theory; on the other hand, it also leaves time of occurrence and direction of the elementary processes a matter of "chance."
It speaks in favor of the theory that the statistical law assumed for [spontaneous] emission is nothing but the Rutherford law of radioactive decay.
[Albert Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/), 1916
The off�-diagonal _n, m_ elements describe the uniquely quantum property of interference between wave functions and provide a measure of the probabilities for transitions between states _n_ and _m_.
It is the intrinsic quantum _probabilities_ that provide the ultimate source of [indeterminism](https://www.informationphilosopher.com/freedom/indeterminism.html), and consequently of irreducible irreversibility, as we shall see.
Transitions between states are irreducibly random, like the decay of a radioactive nucleus (discovered by Rutherford in 1901) or the emission of a photon by an electron transitioning to a lower energy level in an atom (explained by Einstein in 1916).
The axiom of measurement is the formalization of Bohr's 1913 postulate that atomic electrons will be found in stationary states with energies _En_. In 1913, Bohr visualized them as orbiting the nucleus. Later, he said they could not be visualized, but chemists routinely visualize them as clouds of probability amplitude with easily calculated shapes that correctly predict chemical bonding.
The off-diagonal transition probabilities are the formalism of Bohr's "quantum jumps" between his stationary states, emitting or absorbing energy _hν_ = _En_ - _Em_. Einstein explained clearly in 1916 that the jumps are accompanied by his discrete light quanta (photons), but Bohr continued to insist that the radiation was classical for another ten years, deliberately ignoring Einstein's foundational efforts in what Bohr might have felt was his area of expertise (quantum mechanics).
The axiom of measurement asserts that a large number of measurements of the observable _A_, known to have eigenvalues _An_, will result in the number of measurements with value _An_ that is proportional to the probability of fi�nding the system in eigenstate _ψn_.
Quantum mechanics is a probabilistic and statistical theory. The _probabilities_ are theories about what experiments will show. Experiments provide the _statistics_ (the frequency of outcomes) that confirm the predictions of quantum theory - with the highest accuracy of any theory ever discovered!
3. _The Projection Postulate_.
The third novel idea of quantum theory is often considered the most radical. It has certainly produced some of the most radical ideas ever to appear in physics, in attempts by various "interpretations" to deny it.
The projection postulate is actually very simple, and arguably intuitive as well. It says that when a measurement is made, the system of interest will be found in (will instantly "collapse" into) one of the possible eigenstates of the measured observable.
We have several _possibilities_ for eigenvalues. We can calculate the _probabilities_ for each eigenvalue. Measurement simply makes one of these _actual_, and it does so, said Max Born, in proportion to the absolute square of the probability amplitude wave function _ψn_.
Note that [Einstein](https://www.informationphilosopher.com/solutions/scientists/einstein/) saw the chance in quantum theory at least ten years before Born
In this way, ontological chance enters physics, and it is partly this fact of quantum randomness that bothered Einstein ("God does not play dice") and Schrōdinger (whose equation of motion for the probability-amplitude wave function is deterministic).
The projection postulate, or collapse of the wave function, is the element of quantum mechanics most often denied by various "interpretations." The sudden discrete and discontinuous "quantum jumps" are considered so non-intuitive that interpreters have replaced them with the most outlandish (literally) alternatives. The famous "many-worlds interpretation" substitutes a "splitting" of the entire universe into two equally large universes, massively violating the most fundamental conservation principles of physics, rather than allow a diagonal photon arriving at a polarizer to suddenly "collapse" into a horizontal or vertical state.
4.1 _An example of projection_.
Given a quantum system in an initial state | _φ_ >, we can expand it in a linear combination of the eigenstates of our measurement apparatus, the | _ψn_ >.
| _φ_ > = ∑ n = 0 n = ∞ _cn_ | _ψn_ >. (8)
In the case of [Dirac's polarized photons](https://www.informationphilosopher.com/solutions/experiments/dirac_3-polarizers/), the diagonal state | _d_ > is a linear combination of the horizontal and vertical states of the measurement apparatus, | _v_ > and | _h_ >. When we square the (1/√2) coefficients, we see there is a 50% chance of measuring the photon as either horizontal or vertically polarized.
| _d_ > = ( 1/√2) | _v_ > + ( 1/√2) | _h_ > (10)
4.2 _Visualizing projection_.
When a photon is prepared in a vertically polarized state | _v_ >, its interaction with a vertical polarizer is easy to visualize. We can picture the state vector of the whole photon simply passing through the polarizer unchanged.
The same is true of a photon prepared in a horizontally polarized state | _h_ > going through a horizontal polarizer. And the interaction of a horizontal photon with a vertical polarizer is easy to understand. The vertical polarizer will absorb the horizontal photon completely.
The diagonally polarized photon | _d_ >, however, fully reveals the non-intuitive nature of quantum physics. We can visualize quantum [indeterminacy](https://www.informationphilosopher.com/freedom/indeterminacy.html), its [statistical](https://www.informationphilosopher.com/freedom/probability.html) nature, and we can dramatically visualize the process of [collapse](https://www.informationphilosopher.com/solutions/experiments/wave-function_collapse/), as a state vector aligned in one direction must rotate instantaneously into another vector direction.

As we saw above (Figure 2.1), the vector projection of | _d_ > onto | _v_ >, with length (1/√2), gives us the probability 1/2 for photons to emerge from the vertical polarizer. But this is only a statistical statement about the expected probability for large numbers of identically prepared photons.
When we have only one photon at a time, _we never get one-half of a photon_ coming through the polarizer. Critics of standard quantum theory sometimes say that it tells us nothing about individual particles, only ensembles of identical experiments. There is truth in this, but nothing stops us from imagining the strange process of a single diagonally polarized photon interacting with the vertical polarizer.
There are two possibilities. We either get a whole photon coming through (which means that it "collapsed" or the diagonal vector was "reduced to" a vertical vector) or we get no photon at all. This is the entire meaning of "collapse." It is the same as an atom "jumping" discontinuously and suddenly from one energy level to another. It is the same as the photon in a two-slit experiment suddenly appearing at one spot on the photographic plate, where an instant earlier it might have appeared anywhere.
We can even visualize what happens when no photon appears. We can imagine that the diagonal photon was reduced to a horizontally polarized photon and was completely absorbed.
Why can we see the statistical nature and the indeterminacy? First, statistically, in the case of many identical photons, we can say that half will pass through and half will be absorbed.
The indeterminacy is that in the case of one photon, we have no ability to know which it will be. This is just as we cannot predict the time when a radioactive nucleus will decay, or the time and direction of an atom emitting a photon.
This indeterminacy is a consequence of our diagonal photon state vector being "represented" (transformed) into a linear superposition of vertical and horizontal photon state vectors. Thus the _principle of superposition_ together with the _projection postulate_ provides us with indeterminacy, statistics, and a way to "visualize" the collapse of a superposition of quantum states into one of the basis states.